题目内容
已知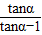 =-1,求下列各式的值:
=-1,求下列各式的值:(1)
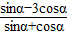 ;
;(2)sin2α+sin αcos α+2.
【答案】分析:由已知得tanα=
(1)由于已知tanα,故考虑把所求的式子化为正切的形式,结合tanα=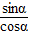 ,可知把所求的式子分子、分母同时除以
,可知把所求的式子分子、分母同时除以
cosα即可
(2)同(1)的思路,但所求式子没有分母,从而先变形为分式的形式,分母添1,而1=sin2α+cos2α,以下同(1)
解答:解:由已知得tanα=
(1)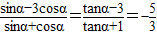
(2)sin2α+sinαcosα+2
=sin2α+sinαcosα+2(cos2α+sin2α)
=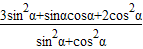
=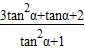
=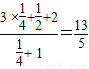
点评:本题主要考查了三角函数求值化简中的常用技巧:已知tanα,求形如①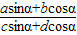 ②asin2α+bsinαcosα+ccos2α,对于①常在分子、分母上同时除以cosα,对于②要先在分母上添上1,1=sin2α+cos2α,然后分子、分母同时除以cos2α,从而把所求的式子化简为含有“切”的形式.
②asin2α+bsinαcosα+ccos2α,对于①常在分子、分母上同时除以cosα,对于②要先在分母上添上1,1=sin2α+cos2α,然后分子、分母同时除以cos2α,从而把所求的式子化简为含有“切”的形式.

(1)由于已知tanα,故考虑把所求的式子化为正切的形式,结合tanα=
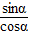 ,可知把所求的式子分子、分母同时除以
,可知把所求的式子分子、分母同时除以cosα即可
(2)同(1)的思路,但所求式子没有分母,从而先变形为分式的形式,分母添1,而1=sin2α+cos2α,以下同(1)
解答:解:由已知得tanα=

(1)
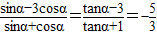
(2)sin2α+sinαcosα+2
=sin2α+sinαcosα+2(cos2α+sin2α)
=
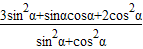
=
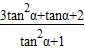
=
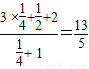
点评:本题主要考查了三角函数求值化简中的常用技巧:已知tanα,求形如①
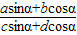 ②asin2α+bsinαcosα+ccos2α,对于①常在分子、分母上同时除以cosα,对于②要先在分母上添上1,1=sin2α+cos2α,然后分子、分母同时除以cos2α,从而把所求的式子化简为含有“切”的形式.
②asin2α+bsinαcosα+ccos2α,对于①常在分子、分母上同时除以cosα,对于②要先在分母上添上1,1=sin2α+cos2α,然后分子、分母同时除以cos2α,从而把所求的式子化简为含有“切”的形式. 
练习册系列答案
相关题目
已知
 ,
, ,求下列各对数的值:
,求下列各对数的值:
|
(1) |
(2) |
|
(3) |
(4) |



