题目内容

函数 $数学公式$ （a＞0，a≠1）的图象恒过定点A，若点A在幂函数f（x）的图象上，则f（8）等于

A.
2
B.
8
C.
$数学公式$
D.
$数学公式$

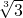
A
分析：先求出点A（-27，-3），设幂函数f（x）的解析式为f（x）=x^α，把点A（-27，-3）代入幂函数的解析式求出α的值，可得幂函数的解析式，从而求得f（8）的值．
解答：函数 $\text{[math]}$ （a＞0，a≠1）的图象恒过定点A（-27，-3），设幂函数f（x）的解析式为f（x）=x^α，
把点A（-27，-3）代入幂函数的解析式可得-3=（-27）^α，∴α= $\text{[math]}$ ，故 f（x）= $\text{[math]}$ ．
∴f（8）= $\text{[math]}$ =2，
故选A．
点评：本题主要考查对数函数的单调性和特殊点，幂函数的定义，求函数的值，属于中档题．

练习册系列答案

夺冠课时导学案系列答案

发现会考系列答案

发展性评价系列答案

仿真试卷系列答案

非常好冲刺系列答案

非考不可年级衔接总复习系列答案

分层学习检测与评价系列答案

普通高中招生考试命题指导纲要系列答案

高分计划系列答案

高效测评单元测评系列答案

相关题目

（2013•普陀区二模）已知a＞0且a≠1，函数f（x）=log_a（x+1），g(x)=loga

，记F（x）=2f（x）+g（x）
（1）求函数F（x）的定义域D及其零点；
（2）若关于x的方程F（x）-m=0在区间[0，1）内有解，求实数m的取值范围．

已知奇函数f（x），偶函数g（x）满足f（x）+g（x）=a^x（a＞0且a≠1）．
（1）求证：f（2x）=2f（x）g（x）；
（2）设f（x）的反函数f-1(x)，当a=

-1时，比较f^-1[g（x）]与-1的大小，证明你的结论；
（3）若a＞1，n∈N*，且n≥2，比较f（n）与nf（1）的大小，并证明你的结论．

已知函数f（x）=a^x+k（a＞0且a≠1）的图象过点（-1，1），其反函数f^-1（x）的图象过点（8，2）．（1）求a，k的值
（2）若将y=f^-1（x）的图象向左平移2个单位，再向上平移1个单位，就得到函数y=g（x）的图象，写出y=g（x）的解析式
（3）若函数F（x）=g（x²）-f^-1（x），求F（x）的最小值及取得最小值时x的值．

已知奇函数f（x），偶函数g（x）满足f（x）+g（x）=a^x（a＞0且a≠1）．
（1）求证：f（2x）=2f（x）g（x）；
（2）设f（x）的反函数f-1(x)，当a=

-1时，比较f^-1[g（x）]与-1的大小，证明你的结论；
（3）若a＞1，n∈N*，且n≥2，比较f（n）与nf（1）的大小，并证明你的结论．

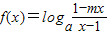（a＞0，a≠1，m≠1）是奇函数．
（1）求实数m的值；
（2）判断函数f（x）在（1，+∞）上的单调性，并给出证明；
（3）当x∈（r，a-2）时，函数f（x）的值域是（1，+∞），求实数r与a的值