题目内容
设函数 .
.
(1)当a=0时,求f(x)的极值;
(2)设 ,在[1,+∞)上单调递增,求a的取值范围;
,在[1,+∞)上单调递增,求a的取值范围;
(3)当a≠0时,求f(x)的单调区间.
 .
.(1)当a=0时,求f(x)的极值;
(2)设
 ,在[1,+∞)上单调递增,求a的取值范围;
,在[1,+∞)上单调递增,求a的取值范围;(3)当a≠0时,求f(x)的单调区间.
解:(1)函数f(x)的定义域为(0,+∞).
当a=0时,f(x)=2lnx+ ,
,
∴f'(x)= ﹣
﹣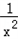 =
=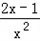 ,
,
由f'(x)=0得x= ,
,
于是,f(x),f'(x)随x变化如下表:

故,f(x)极小值=f( )=2﹣ln2,没有极大值.
)=2﹣ln2,没有极大值.
(2)由题意,g(x)=(2﹣a)lnx+2ax,在[1,+∞)上单调递增,
∴g'(x)=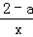 +2a≥0在[1,+∞)上恒成立,设h(x)=2ax+2﹣a≥0在[1,+∞)上恒成立,
+2a≥0在[1,+∞)上恒成立,设h(x)=2ax+2﹣a≥0在[1,+∞)上恒成立,
当a=0时,2≥0恒成立,符合题意.
当a>0时,h(x)在[1,+∞)上单调递增,h(x)的最小值为h(1)=2a+2﹣a≥0,
得a≥﹣2,所以a>0
当a<0时,h(x)在[1,+∞)上单调递减,不合题意
所以a≥0
(3)由题意得,f'(x)=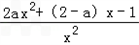 ,
,
令f'(x)=0得x1=﹣ ,x2=
,x2= ,
,
若a>0,由f'(x)≤0得x∈(0, ];
];
由f'(x)≥0得x∈[ ,+∞);
,+∞);
若a<0,①当a<﹣2时,0<﹣ <
< ,x∈(0,﹣
,x∈(0,﹣ ]或x∈[
]或x∈[ ,+∞),f'(x)≤0;x∈[﹣
,+∞),f'(x)≤0;x∈[﹣ ,
, ],f'(x)≥0,
],f'(x)≥0,
②当a=﹣2时,f'(x)≤0;
③当﹣2<a<0时,﹣ >
> ,x∈(0,
,x∈(0, ]或x∈[﹣
]或x∈[﹣ ,+∞),f'(x)≤0;x∈[
,+∞),f'(x)≤0;x∈[ ,﹣
,﹣ ],f'(x)≥0.
],f'(x)≥0.
综上,当a>0时,函数的单调递减区间为(0, ],单调递增区间为[
],单调递增区间为[ ,+∞);
,+∞);
当a<﹣2时,函数的单调递减区间为(0,﹣ ],[
],[ ,+∞),单调递增区间为[﹣
,+∞),单调递增区间为[﹣ ,
, ];
];
当a=﹣2时,函数的单调递减区间为(0,+∞);
当﹣2<a<0时,函数的单调递减区间为(0, ],[﹣
],[﹣ ,+∞),单调递增区间为[
,+∞),单调递增区间为[ ,﹣
,﹣ ].
].
当a=0时,f(x)=2lnx+
 ,
, ∴f'(x)=
 ﹣
﹣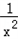 =
=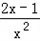 ,
,由f'(x)=0得x=
 ,
,于是,f(x),f'(x)随x变化如下表:

故,f(x)极小值=f(
 )=2﹣ln2,没有极大值.
)=2﹣ln2,没有极大值.(2)由题意,g(x)=(2﹣a)lnx+2ax,在[1,+∞)上单调递增,
∴g'(x)=
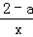 +2a≥0在[1,+∞)上恒成立,设h(x)=2ax+2﹣a≥0在[1,+∞)上恒成立,
+2a≥0在[1,+∞)上恒成立,设h(x)=2ax+2﹣a≥0在[1,+∞)上恒成立,当a=0时,2≥0恒成立,符合题意.
当a>0时,h(x)在[1,+∞)上单调递增,h(x)的最小值为h(1)=2a+2﹣a≥0,
得a≥﹣2,所以a>0
当a<0时,h(x)在[1,+∞)上单调递减,不合题意
所以a≥0
(3)由题意得,f'(x)=
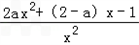 ,
,令f'(x)=0得x1=﹣
 ,x2=
,x2= ,
,若a>0,由f'(x)≤0得x∈(0,
 ];
];由f'(x)≥0得x∈[
 ,+∞);
,+∞);若a<0,①当a<﹣2时,0<﹣
 <
< ,x∈(0,﹣
,x∈(0,﹣ ]或x∈[
]或x∈[ ,+∞),f'(x)≤0;x∈[﹣
,+∞),f'(x)≤0;x∈[﹣ ,
, ],f'(x)≥0,
],f'(x)≥0,②当a=﹣2时,f'(x)≤0;
③当﹣2<a<0时,﹣
 >
> ,x∈(0,
,x∈(0, ]或x∈[﹣
]或x∈[﹣ ,+∞),f'(x)≤0;x∈[
,+∞),f'(x)≤0;x∈[ ,﹣
,﹣ ],f'(x)≥0.
],f'(x)≥0.综上,当a>0时,函数的单调递减区间为(0,
 ],单调递增区间为[
],单调递增区间为[ ,+∞);
,+∞);当a<﹣2时,函数的单调递减区间为(0,﹣
 ],[
],[ ,+∞),单调递增区间为[﹣
,+∞),单调递增区间为[﹣ ,
, ];
];当a=﹣2时,函数的单调递减区间为(0,+∞);
当﹣2<a<0时,函数的单调递减区间为(0,
 ],[﹣
],[﹣ ,+∞),单调递增区间为[
,+∞),单调递增区间为[ ,﹣
,﹣ ].
].
练习册系列答案
相关题目
 。
。 的极值;
的极值; 2时,讨论函数
2时,讨论函数 成立,求
成立,求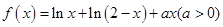 。
。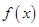 的单调区间。
的单调区间。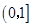 上的最大值为
上的最大值为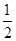 ,求a的值。
,求a的值。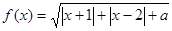 。
。 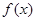 的定义域。
的定义域。 。
。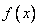 的单调区间。
的单调区间。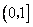 上的最大值为
上的最大值为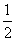 ,求a的值。
,求a的值。