题目内容
已知△ABC中，条件甲：tanA=
，条件乙：△ABC为等边三角形，则甲是乙的（ ）
| 2cosC+cosA |
| 2sinC-sinA |
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分又不必要条件 |
甲：在△ABC中，由于tanA=
，则
=
，
整理得：2（cosAcosC-sinAsinC）=-1，即cos（A+C）=-
，
又由cos（B）=-cos（A+C）=
，则∠B=60°；
乙：由于△ABC为等边三角形，则∠A=∠B=∠C=60°．
由于甲?乙为假命题，乙?甲为真命题，则甲是乙的必要不充分条件．
故选B．
| 2cosC+cosA |
| 2sinC-sinA |
| sinA |
| cosA |
| 2cosC+cosA |
| 2sinC-sinA |
整理得：2（cosAcosC-sinAsinC）=-1，即cos（A+C）=-
| 1 |
| 2 |
又由cos（B）=-cos（A+C）=
| 1 |
| 2 |
乙：由于△ABC为等边三角形，则∠A=∠B=∠C=60°．
由于甲?乙为假命题，乙?甲为真命题，则甲是乙的必要不充分条件．
故选B．
练习册系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
，条件乙：△ABC为等边三角形，则甲是乙的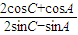
，条件乙：△ABC为等边三角形，则甲是乙的（ ）
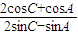，条件乙：△ABC为等边三角形，则甲是乙的（ ）