题目内容
试由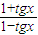
=1+sin2x，求的x通值．
【答案】分析：先根据正切函数与正余弦函数的关系将正切函数化为正余弦函数之比，然后再用二倍角公式和同角三角函数的基本关系进行整理化简，从而可得到2（cosx+sinx）•sin2x=0，最后根据三角函数的基本性质可求得x的值．
解答：解：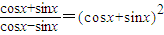
（cosx+sinx）（1-cos2x+sin2x）=0
2（cosx+sinx）•sin2x=0
∴cosx+sinx=0，即tgx=-1∴x=kπ-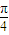
或sin2x=0∴x=kπ（k为整数）
由检验可知，均为其通解．
点评：本题主要考查同角三角函数的基本关系和二倍角公式的应用．考查对三角函数的基本知识和基本性质的运用，三角函数的知识点比较多，内容比较琐碎，一定要在平时注意多积累多练习．
解答：解：
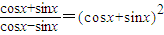
（cosx+sinx）（1-cos2x+sin2x）=0
2（cosx+sinx）•sin2x=0
∴cosx+sinx=0，即tgx=-1∴x=kπ-
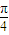
或sin2x=0∴x=kπ（k为整数）
由检验可知，均为其通解．
点评：本题主要考查同角三角函数的基本关系和二倍角公式的应用．考查对三角函数的基本知识和基本性质的运用，三角函数的知识点比较多，内容比较琐碎，一定要在平时注意多积累多练习．
练习册系列答案
相关题目
（A＞0，ω＞0）图象上的一个最高点的坐标为（
），则此点到相邻最低点间的曲线与x轴交于点（
），若φ∈（
）．