题目内容
(本小题满分14分)已知椭圆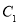 的中心在坐标原点,两焦点分别为双曲线
的中心在坐标原点,两焦点分别为双曲线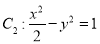 的顶点,直线
的顶点,直线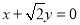 与椭圆
与椭圆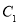 交于
交于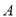 ,
, 两点,且点
两点,且点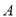 的坐标为
的坐标为 ,点
,点 是椭圆
是椭圆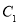 上异于点
上异于点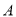 ,
,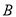 的任意一点,点
的任意一点,点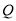 满足
满足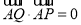 ,
, ,且
,且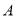 ,
,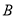 ,
,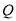 三点不共线.
三点不共线.
(1)求椭圆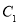 的方程;
的方程;
(2)求点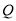 的轨迹方程;
的轨迹方程;
(3)求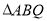 面积的最大值及此时点
面积的最大值及此时点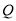 的坐标.
的坐标.
(1)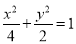 ;
;
(2)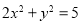 ,除去四个点
,除去四个点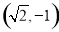 ,
,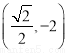 ,
,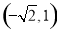 ,
,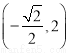 ;
;
(3)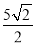 ,点
,点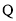 的坐标为
的坐标为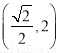 或
或 .
.
【解析】
试题分析:(1)由双曲线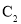 的顶点得椭圆
的顶点得椭圆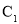 的焦点,由椭圆的定义得
的焦点,由椭圆的定义得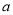 的值,利用
的值,利用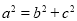 即可得椭圆
即可得椭圆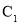 的方程;(2)设点
的方程;(2)设点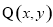 ,先写出
,先写出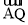 ,
,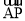 ,
,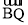 ,
, 的坐标,再根据已知条件可得
的坐标,再根据已知条件可得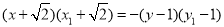 ,
,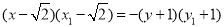 ,代入,化简,即可得点
,代入,化简,即可得点 的轨迹方程;(3)先计算
的轨迹方程;(3)先计算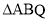 的面积
的面积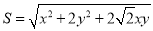 ,利用基本不等式即可得
,利用基本不等式即可得 的面积的最大值.
的面积的最大值.
试题解析:(1)解法1: ∵ 双曲线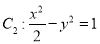 的顶点为
的顶点为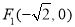 ,
,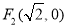 , 1分
, 1分
∴ 椭圆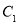 两焦点分别为
两焦点分别为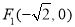 ,
,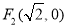 .
.
设椭圆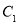 方程为
方程为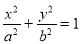
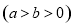 ,
,
∵ 椭圆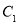 过点
过点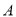
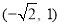 ,
,
∴ 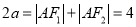 ,得
,得 . 2分
. 2分
∴ 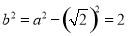 . 3分
. 3分
∴ 椭圆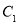 的方程为
的方程为 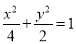 . 4分
. 4分
解法2: ∵ 双曲线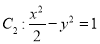 的顶点为
的顶点为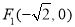 ,
,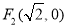 , 1分
, 1分
∴ 椭圆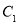 两焦点分别为
两焦点分别为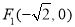 ,
,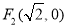 .
.
设椭圆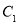 方程为
方程为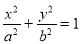
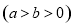 ,
,
∵ 椭圆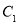 过点
过点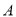
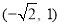 ,
,
∴ 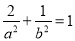 . ① 2分
. ① 2分
∵ 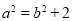 , ② 3分
, ② 3分
由①②解得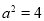 ,
, 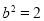 .
.
∴ 椭圆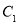 的方程为
的方程为 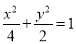 . 4分
. 4分
(2)解法1:设点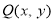 ,点
,点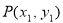 ,
,
由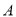
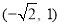 及椭圆
及椭圆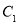 关于原点对称可得
关于原点对称可得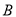
 ,
,
∴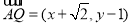 ,
,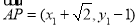 ,
,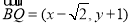 ,
,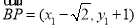 .
.
由 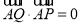 , 得
, 得  , 5分
, 5分
即 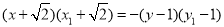 . ①
. ①
同理, 由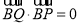 , 得
, 得 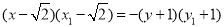 . ② 6分
. ② 6分
①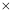 ②得
②得 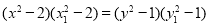 . ③ 7分
. ③ 7分
由于点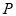 在椭圆
在椭圆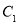 上, 则
上, 则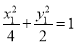 ,得
,得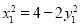 ,
,
代入③式得 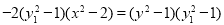 .
.
当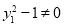 时,有
时,有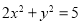 ,
,
当 ,则点
,则点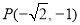 或
或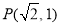 ,此时点
,此时点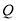 对应的坐标分别为
对应的坐标分别为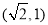 或
或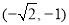 ,其坐标也满足方程
,其坐标也满足方程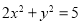 . 8分
. 8分
当点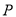 与点
与点 重合时,即点
重合时,即点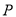
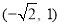 ,由②得
,由②得 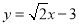 ,
,
解方程组 得点
得点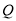 的坐标为
的坐标为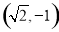 或
或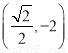 .
.
同理, 当点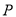 与点
与点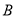 重合时,可得点
重合时,可得点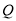 的坐标为
的坐标为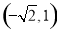 或
或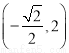 .
.
∴点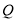 的轨迹方程为
的轨迹方程为 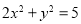 , 除去四个点
, 除去四个点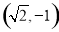 ,
,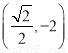 ,
, 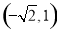 ,
,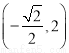 . 9分
. 9分
解法2:设点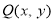 ,点
,点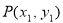 ,
,
由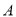
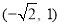 及椭圆
及椭圆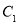 关于原点对称可得
关于原点对称可得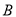
 ,
,
∵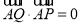 ,
,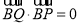 ,
,
∴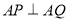 ,
,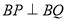 .
.
∴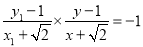
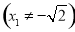 ,① 5分
,① 5分

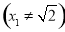 . ② 6分
. ② 6分
①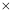 ② 得
② 得  . (*) 7分
. (*) 7分
∵ 点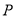 在椭圆
在椭圆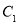 上, ∴
上, ∴ 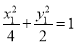 ,得
,得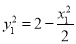 ,
,
代入(*)式得 ,即
,即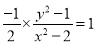 ,
,
化简得 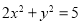 .
.
若点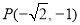 或
或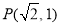 , 此时点
, 此时点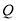 对应的坐标分别为
对应的坐标分别为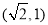 或
或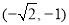 ,其坐标也满足方程
,其坐标也满足方程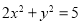 . 8分
. 8分
当点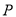 与点
与点 重合时,即点
重合时,即点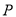
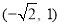 ,由②得
,由②得 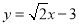 ,
,
解方程组 得点
得点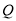 的坐标为
的坐标为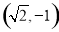 或
或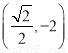 .
.
同理, 当点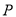 与点
与点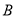 重合时,可得点
重合时,可得点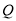 的坐标为
的坐标为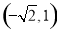 或
或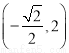 .
.
∴点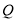 的轨迹方程为
的轨迹方程为 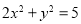 , 除去四个点
, 除去四个点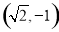 ,
,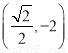 ,
, 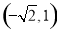 ,
,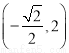 . 9分
. 9分
(3) 解法1:点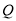
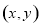 到直线
到直线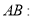
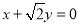 的距离为
的距离为 .
.
△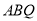 的面积为
的面积为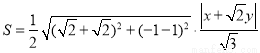 10分
10分
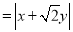
 . 11分
. 11分
而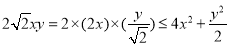 (当且仅当
(当且仅当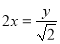 时等号成立)
时等号成立)
∴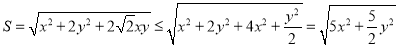
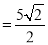 . 12分
. 12分
当且仅当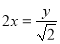 时, 等号成立.
时, 等号成立.
由 解得
解得 或
或 13分
13分
∴△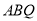 的面积最大值为
的面积最大值为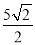 , 此时,点
, 此时,点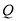 的坐标为
的坐标为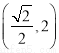 或
或 . 14分
. 14分
解法2:由于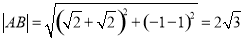 ,
,
故当点 到直线
到直线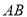 的距离最大时,△
的距离最大时,△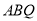 的面积最大. 10分
的面积最大. 10分
设与直线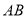 平行的直线为
平行的直线为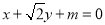 ,
,
由 消去
消去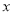 ,得
,得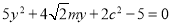 ,
,
由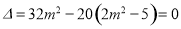 ,解得
,解得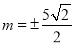 . 11分
. 11分
若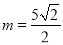 ,则
,则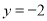 ,
,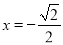 ;若
;若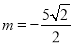 ,则
,则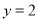 ,
,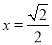 . 12分
. 12分
故当点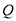 的坐标为
的坐标为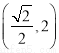 或
或 时,△
时,△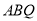 的面积最大,其值为
的面积最大,其值为
 . 14分
. 14分
考点:1、椭圆的方程;2、双曲线的方程;3、直线与圆锥曲线;4、基本不等式;5、三角形的面积;6、动点的轨迹方程.
考点分析: 考点1:椭圆的标准方程 考点2:椭圆的几何性质 试题属性- 题型:
- 难度:
- 考核:
- 年级:

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 .
. 的解集;
的解集;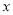 的不等式
的不等式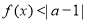 的解集非空,求实数
的解集非空,求实数 的取值范围.
的取值范围. ,则输出的
,则输出的 为( )
为( )
 B.
B.
 D.
D.
 服从正态分布
服从正态分布 ,
, ,则
,则 .
.
 B.
B.
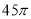 D.
D.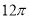
 是圆
是圆 的一条弦,延长
的一条弦,延长 至点
至点 ,使得
,使得 ,过
,过 作圆
作圆 为切点,
为切点, 的平分线
的平分线 交
交 于点
于点 ,则
,则 的长为 .
的长为 .
 是全体复数构成的集合,若映射
是全体复数构成的集合,若映射 R满足: 对任意
R满足: 对任意 ,以及任意
,以及任意 R , 都有
R , 都有 , 则称映射
, 则称映射 具有性质
具有性质 . 给出如下映射:
. 给出如下映射: R ,
R ,  ,
,  i
i R
R ;
; R ,
R ,  ,
,  R ,
R ,  ,
,  中,
中, 是
是 边上一点,
边上一点, ,则
,则 的长为
的长为 
 和
和 的图像关于原点对称,且
的图像关于原点对称,且
 的解析式;
的解析式; 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.