题目内容
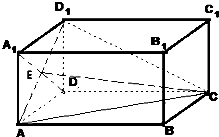 如图,长方体ABCD-A1B1C1D1中,AB=2,A1A=AD=1,E为AD1与A1D的交点.
如图,长方体ABCD-A1B1C1D1中,AB=2,A1A=AD=1,E为AD1与A1D的交点.(1)求二面角C-AD1-D 的平面角正切值.
(2)求D点到平面ACD1的距离.
分析:(1)在长方体ABCD-A1B1C1D1中,以D为坐标原点,以DA、DC、DD1所在直线为x轴、y轴、z轴建立空间直角坐标系,求出两个平面AD1D与AD1C的一个法向量,由两个法向量所成的角的余弦值求二面角的余弦值,从而求出正切值;
(2)在(1)中求出了AD1C的一个法向量,E点是平面AD1C上的一个点,求出向量
,则向量
在平面AD1C的一个法向量上的投影的绝对值即为点D到平面ACD1的距离.
(2)在(1)中求出了AD1C的一个法向量,E点是平面AD1C上的一个点,求出向量
| ED |
| ED |
解答:解:(1)如图,
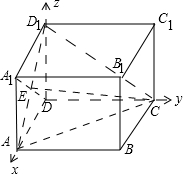
以DA、DC、DD1所在直线为x轴、y轴、z轴建立空间直角坐标系,
因为AB=2,A1A=AD=1,E为AD1与A1D的交点,
所以,A(1,0,0),C(0,2,0),D1(0,0,1),
E(
,0,
),D(0,0,0).
=(-1,2,0),
=(0,2,-1),
=(-
,0,-
).
则平面AD1D的一个法向量为
=(2,0,0),
设平面AD1C的一个法向量
=(x,y,z),
由
,得
,取y=1,则x=z=2,
所以
=(2,1,2).
再设二面角C-AD1-D 的平面角为θ,
则cosθ=
=
=
.
所以sinθ=
=
=
.
则二面角C-AD1-D 的平面角正切值为tanθ=
=
=
.
(2)D点到平面AD1C的距离为d=
=
=
.
所以D点到平面ACD1的距离为
.

以DA、DC、DD1所在直线为x轴、y轴、z轴建立空间直角坐标系,
因为AB=2,A1A=AD=1,E为AD1与A1D的交点,
所以,A(1,0,0),C(0,2,0),D1(0,0,1),
E(
| 1 |
| 2 |
| 1 |
| 2 |
| AC |
| D1C |
| ED |
| 1 |
| 2 |
| 1 |
| 2 |
则平面AD1D的一个法向量为
| DC |
设平面AD1C的一个法向量
| n |
由
|
|
所以
| n |
再设二面角C-AD1-D 的平面角为θ,
则cosθ=
| ||||
|
|
| 4+1×0+2×0 | ||||
|
| 2 |
| 3 |
所以sinθ=
| 1-cos2θ |
1-(
|
| ||
| 3 |
则二面角C-AD1-D 的平面角正切值为tanθ=
| sinθ |
| cosθ |
| ||||
|
| ||
| 2 |
(2)D点到平面AD1C的距离为d=
|
| ||||
|
|
|(-
| ||||
|
| 2 |
| 3 |
所以D点到平面ACD1的距离为
| 2 |
| 3 |
点评:本题考查了空间中的点线面的角及距离的计算,考查了向量法,利用向量法求解空间角和距离的关键是在理解的基础上熟记有关公式,该题是中档题.

练习册系列答案
相关题目
 19、如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
19、如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点. 15、如图,长方体ABCD-A1B1C1D1中被截去一部分,
15、如图,长方体ABCD-A1B1C1D1中被截去一部分, 如图在长方体ABCD-A1B1C1D1中,其中AB=BC,E,F分别是AB1,BC1的中点,则以下结论中
如图在长方体ABCD-A1B1C1D1中,其中AB=BC,E,F分别是AB1,BC1的中点,则以下结论中 如图,长方体ABCD-A1B1C1D1中,P是线段AC的中点.
如图,长方体ABCD-A1B1C1D1中,P是线段AC的中点.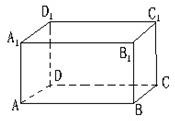 已知如图:长方体ABCD-A1B1C1D1中,交于顶点A的三条棱长别为AD=3,AA1=4,AB=5.一天,小强观察到在A处有一只蚂蚁,发现顶点C1处有食物,于是它沿着长方体的表面爬行去获取食物,则蚂蚁爬行的最短路程是( )
已知如图:长方体ABCD-A1B1C1D1中,交于顶点A的三条棱长别为AD=3,AA1=4,AB=5.一天,小强观察到在A处有一只蚂蚁,发现顶点C1处有食物,于是它沿着长方体的表面爬行去获取食物,则蚂蚁爬行的最短路程是( )