题目内容
【题目】若无穷数列![]() 满足:
满足:![]() ,且对任意
,且对任意![]() ,
,![]() (s,k,l,
(s,k,l,![]() )都有
)都有![]() ,则称数列
,则称数列![]() 为“T”数列.
为“T”数列.
(1)证明:正项无穷等差数列![]() 是“T”数列;
是“T”数列;
(2)记正项等比数列![]() 的前n项之和为
的前n项之和为![]() ,若数列
,若数列![]() 是“T”数列,求数列
是“T”数列,求数列![]() 公比的取值范围;
公比的取值范围;
(3)若数列![]() 是“T”数列,且数列
是“T”数列,且数列![]() 的前n项之和
的前n项之和![]() 满足
满足![]() ,求证:数列
,求证:数列![]() 是等差数列.
是等差数列.
【答案】(1)答案见解析.(2)![]() .(3)答案见解析
.(3)答案见解析
【解析】
(1)![]() ,根据题意得到
,根据题意得到![]() ,得到证明.
,得到证明.
(2)讨论![]() ,
,![]() ,
,![]() 三种情况,
三种情况,![]() 时,计算
时,计算![]() ,
,![]() 时,计算
时,计算![]() ,得到答案.
,得到答案.
(3)计算得到![]() ,根据题意得到
,根据题意得到![]() ,利用退项相减得到
,利用退项相减得到![]() ,得到证明.
,得到证明.
(1)![]() ,
,
因为正项无穷等差数列![]() ,所以
,所以![]() ,且
,且![]() ,所以
,所以![]() ,
,
所以正项无穷等差数列![]() 是“T”数列.
是“T”数列.
(2)1°![]() 时
时![]() 成立,所以
成立,所以![]() ;
;
2°![]() 时
时![]() ,
,
因为![]() ,所以
,所以![]() ,又因为
,又因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以![]() ,所以
,所以![]() .
.
3°![]() 时,
时,
![]()
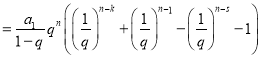 ,
,
因为![]() ,所以
,所以![]() ,又因为
,又因为![]() ,所以
,所以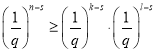 ,
,
所以
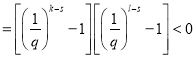 ,
,
所以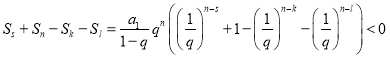 舍去,
舍去,
综上:![]()
(3)![]() ,
,![]() ,
,
所以![]() ,
,
数列![]() 是“T”数列,故
是“T”数列,故![]() ,
,![]() ,…,
,…,![]() ,
,
所以![]() ,所以
,所以![]() ,又因为
,又因为![]() ,所以
,所以![]() ,
,
即![]() ,
,![]() ,相减得到
,相减得到![]() ,
,
故![]() ,相减得到
,相减得到![]() ,故数列
,故数列![]() 是等差数列.
是等差数列.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目