题目内容
设函数
(1)解不等式 ;
;
(2)若关于 的不等式
的不等式 的解集不是空集,求
的解集不是空集,求 得取值范围.
得取值范围.
(1) ;(2)
;(2) 或
或 .
.
解析试题分析:本题考查绝对值不等式的解法和有解问题的求法,考查学生运用函数零点分类讨论的解题思想和转化思想.第一问,利用函数零点分成3类不等式组;第二问,是有解问题,将问题转化为 ,本问的关键是求
,本问的关键是求 ,将函数
,将函数 去掉绝对值,化成分段函数,通过数形结合求出
去掉绝对值,化成分段函数,通过数形结合求出 ,即
,即 ,下面解绝对值不等式求出
,下面解绝对值不等式求出 的取值范围.
的取值范围.
试题解析:(1)∵  ,
,
∴  或
或  或
或 ,
,
∴ 或
或  或
或  ,
,
∴ 或
或 或
或  ,
,
∴ 或
或 . 5分
. 5分
(2)因为 ,
,
所以 ,
,
所以若 的解集不是空集,则
的解集不是空集,则 ,
,
解得: 或
或 ,
,
即 的取值范围是:
的取值范围是: 或
或 . 10分
. 10分
考点:1.绝对值不等式的解法;2.分段函数的最值;3.有解问题的解法.

练习册系列答案
相关题目
 .
. 的定义域为集合
的定义域为集合 ,
, 的定义域为集合
的定义域为集合 ,集合
,集合
 ,求实数
,求实数 的取值范围.
的取值范围. 为真命题,求实数
为真命题,求实数 (
( ),
), .
. 时,求
时,求 ;
; ,求实数
,求实数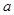 的取值范围.
的取值范围. ,
, .
. ,
, ;
; ,若
,若 ,求实数
,求实数 的取值集合.
的取值集合. ≥1},集合B={x∈R|y=
≥1},集合B={x∈R|y= },若A∪B=A,求实数m的取值范围.
},若A∪B=A,求实数m的取值范围. ,
,
 时,求
时,求 ;
; ,求实数
,求实数 的取值范围.
的取值范围. ,集合B=
,集合B=
 时,求
时,求 ;(2)若
;(2)若 ,求
,求 的取值范围.
的取值范围. B
B
 B
B 求实数a的值;
求实数a的值; B=A求实数a的取值范围;
B=A求实数a的取值范围;