题目内容
(1)用lg2和lg3表示lg75;(2)用logax,logay,logaz表示loga .
.
解:(1)lg75=lg(25×3)=lg(52×3)=2lg5+lg3=2lg![]() +lg3=2(1-lg2)+lg3=2-2lg2+lg3.
+lg3=2(1-lg2)+lg3=2-2lg2+lg3.
(2)原式=loga(x4·![]() )-loga
)-loga![]() =4logax+
=4logax+![]() loga(y2z)-
loga(y2z)-![]() loga(xyz3)
loga(xyz3)
=4logax+![]() (2logay+logaz)-
(2logay+logaz)-![]() (logax+logay+3logaz)
(logax+logay+3logaz)
=![]() logax+
logax+![]() logay-
logay-![]() logaz.
logaz.
点评:用已知对数表示未知对数,就是把要表示的对数的真数分解成已知对数的真数的积、商、幂的形式,然后用对数的运算性质.注意运算性质只有在同底的情况下才能运用.第(2)题中没有指明a、x、y、z的范围,这时我们就认为是使每个对数符号都有意义的a、x、y、z的最大范围,即a>0且a≠1,x>0,y>0,z>0.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 ,圆
,圆 :
: 与
与 轴正半轴的交点为
轴正半轴的交点为 ,与曲线
,与曲线 的交点为
的交点为 ,直线
,直线 与
与 轴的交点为
轴的交点为 .
. 表示
表示 和
和 ;
; ;
; ,
, ,求证:
,求证: .
. 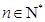 ,圆
,圆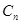 :
: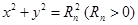 与
与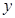 轴正半轴的交点为
轴正半轴的交点为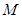 ,与曲线
,与曲线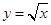 的交点为
的交点为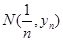 ,直线
,直线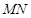 与
与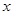 轴的交点为
轴的交点为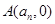 .
.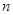 表示
表示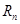 和
和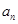 ;
;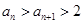 ;
;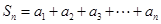 ,
,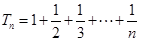 ,求证:
,求证: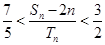 .
.