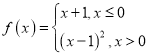题目内容
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,短轴的两个端点分别为A,B,且满足:
,短轴的两个端点分别为A,B,且满足:![]() ,且椭圆经过点
,且椭圆经过点![]()
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过点M![]() 的动直线
的动直线![]() (与X轴不重合)与椭圆C相交于P,Q两点,在X轴上是否存在一定点T,无论直线
(与X轴不重合)与椭圆C相交于P,Q两点,在X轴上是否存在一定点T,无论直线![]() 如何转动,点T始终在以PQ为直径的圆上?若有,求点T的坐标,若无,说明理由。
如何转动,点T始终在以PQ为直径的圆上?若有,求点T的坐标,若无,说明理由。
【答案】(1)![]() ;(2)(2,0)
;(2)(2,0)
【解析】
(1)由![]() 可知,
可知,![]() ,根据椭圆过点
,根据椭圆过点![]() ,即可求出
,即可求出![]() ,由此得到椭圆的标准方程;
,由此得到椭圆的标准方程;
(2)分别讨论直线斜率存在与不存在两种情况,当斜率不存在时,联立直线与椭圆方程,解出![]() 、
、![]() 两点坐标,利用向量垂直的条件可得点
两点坐标,利用向量垂直的条件可得点![]() ,当斜率存在时,设出直线的点斜式,与椭圆联立方程,得到关于
,当斜率存在时,设出直线的点斜式,与椭圆联立方程,得到关于![]() 的一元二次方程,写出根与系数的关系,代入
的一元二次方程,写出根与系数的关系,代入![]() 中进行化简,即可得到答案。
中进行化简,即可得到答案。
(1)由![]() 可知,
可知,![]() ,又椭圆经过点
,又椭圆经过点![]() ,则
,则![]() ,由于在椭圆中
,由于在椭圆中![]() ,所以
,所以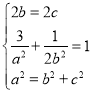 , 解得
, 解得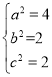 =2,所求椭圆方程为
=2,所求椭圆方程为![]()
(2) 设![]() ,
,![]() ,则
,则![]() ,
,![]()
①当直线![]() 斜率不存在时,则直线
斜率不存在时,则直线![]() 的方程为:
的方程为:![]() ,
,
联立方程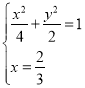 ,解得:
,解得: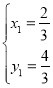 或
或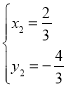 ,故点
,故点![]() ,
,![]() ;
;
则![]() ,
,![]()
由于点![]() 始终在以
始终在以![]() 为直径的圆上,则
为直径的圆上,则![]() ,解得:
,解得:![]() 或
或![]() ,故点
,故点![]() 或
或![]() ;
;
②当直线![]() 斜率
斜率![]() 存在时,设直线
存在时,设直线![]() 的方程为:
的方程为:![]() ,代入椭圆方程
,代入椭圆方程![]() 中消去
中消去![]() 得
得![]() ,
,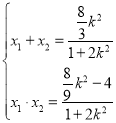
![]()
由于点![]() 始终在以
始终在以![]() 为直径的圆上,
为直径的圆上,
![]()
![]()
![]() ,
,
![]()
 解得:
解得:![]() ,故点
,故点![]() 为
为![]()
综上所述;当![]() 时满足条件。所以定点
时满足条件。所以定点![]() 为
为![]() 。
。

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目