题目内容
(本小题满分14分)如图,已知椭圆 的左焦点为F(
的左焦点为F( ,0),过点M(-3,0)作一条斜率大于0的直线
,0),过点M(-3,0)作一条斜率大于0的直线 与椭圆W交于不同的两点A、B,延长BF交椭圆W于点C.
与椭圆W交于不同的两点A、B,延长BF交椭圆W于点C.

(1)求椭圆W的离心率;
(2)若∠MAC=60°,求直线 的斜率.
的斜率.
(1) (2)
(2) .
.
【解析】
试题分析:(1)由 解得
解得 ,可求得椭圆方程为
,可求得椭圆方程为 ,所以可求其离心率;(2)设出直线方程,并将直线方程与椭圆方程联立,可得
,所以可求其离心率;(2)设出直线方程,并将直线方程与椭圆方程联立,可得 坐标与斜率
坐标与斜率 的关系,由坐标关系可得点
的关系,由坐标关系可得点 关于
关于 轴的对称点为
轴的对称点为 ,可得
,可得 ,即
,即 为等边三角形,可求得
为等边三角形,可求得 .
.
试题解析:(1)由题设 ,
,
解得 ,(3分)
,(3分)
所以椭圆W: ,
,
离心率 .(5分)
.(5分)

(2)设直线 的方程为
的方程为 .
.
联立
得 ,
,
由直线 与椭圆W交于A、B两点,可知
与椭圆W交于A、B两点,可知
△ ,解得
,解得 ,
,
设点A,B的坐标分别为 ,
,
则 ,
, ,(8分)
,(8分)
因为F(-2,0),设点A关于 轴的对称点为C′,则C′(
轴的对称点为C′,则C′( ),
),
所以 ,
,
又因为


 ,
,
所以B,F,C′共线,从而C与C′重合,
连接MC,则 ,(12分)
,(12分)
则△MAC为等边三角形,所以直线 的斜率
的斜率 ,符合
,符合 ,
,
综上,直线 的斜率为
的斜率为 .(14分)
.(14分)
考点:椭圆定义及几何性质,直线与椭圆位置关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的圆心和半径分别为( )
的圆心和半径分别为( )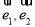 为互相垂直的两个单位向量,则
为互相垂直的两个单位向量,则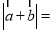 ( )
( )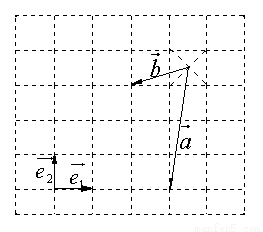
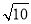 C.
C.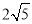 D.
D.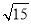
 ,
, ,若
,若 ,则
,则 =__________.
=__________.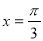 ”是“
”是“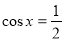 ”成立的( )
”成立的( ) 的前
的前 项和记为
项和记为 ,若
,若 ,
, ,则数列
,则数列 的通项公式为
的通项公式为 _______________.
_______________. 为非零常数,则“
为非零常数,则“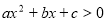 与
与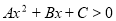 解集相同”是“
解集相同”是“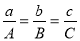 ”的
”的 ,则
,则 .
. ,
, , ,
, , ,则抽取的
,则抽取的 人中,编号在区间
人中,编号在区间 内的人数是 .
内的人数是 .