Question

已知集合A=｛x||x-a|＜ax,a＞0｝若f(x)=sinπx-cosπx在A上是增函数，求a的最大值.

Answer 1

分析：由f(x)在A上是增函数，知A应包含于f(x)的增区间，故需化简A，求f(x)的单调增区间.

解：由|x-a|＜ax得

∴      (a＞0)

    当1-a＞0，即0＜a＜1时，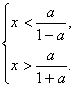

∴A={x|＜x＜}.

f(x)=sin(πx-),由2kπ-≤πx-≤2kπ+得

2k-≤x≤2k+.

∵f(x)在A上为增函数，

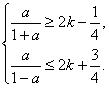∴  (k∈Z).

∵0＜＜1，＞1,∴k=0.

∴

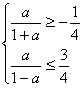
∴0＜a≤,即a的最大值为,

    当1-a＜0即a＞1时，A=｛x|x＞｝,与f(x)在A上单调增不符；

    当1-a=0,即a=1时，A=｛x|x＞｝,与f(x)在A上单调增不符.

    综上得a的最大值为.