题目内容
 已知
已知| a |
| b |
| a |
| b |
| π |
| 4 |
(1)求m、n的值;
(2)用五点法画出f(x)在一个周期内的大致图象.
(3)若函数g(x)=af(x)+1在区间[-
| π |
| 4 |
| π |
| 4 |
分析:(1)先求得f(x)=mcos2x+nsin2x,再根据它的图象过 (0,1),(
,1),求得m和n的值.
(2)由(1)可得 f(x)=sin2x+cos2x=
sin(2x+
),再用五点法作出它在一个周期上的简图.
(3)根据正弦函数的定义域和值域,结合函数g(x)=af(x)+1在区间[-
,
]上的最大值与最小值之和为3,求得a的值.
| π |
| 4 |
(2)由(1)可得 f(x)=sin2x+cos2x=
| 2 |
| π |
| 4 |
(3)根据正弦函数的定义域和值域,结合函数g(x)=af(x)+1在区间[-
| π |
| 4 |
| π |
| 4 |
解答:解:(1)求得f(x)=mcos2x+nsin2x,再根据它的图象过 (0,1),(
,1),求得m=1,n=1.
(2)由(1)可得 f(x)=sin2x+cos2x=
sin(2x+
),
列表:
如图: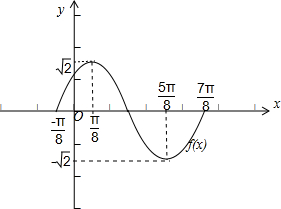
(3)∵g(x)=
sin(2x+
)+1,-
≤x≤
,∴-
≤2x+
≤
π,
∴-1≤
sin(2x+
)≤
,-a≤
asin(2x+
)≤
a(a>0),
或a<0,
a≤
asin(2x+
)≤-a,
∴
a-a+2=3,a=
+1.
| π |
| 4 |
(2)由(1)可得 f(x)=sin2x+cos2x=
| 2 |
| π |
| 4 |
列表:
2x+
|
0 |
|
π |
|
2π | ||||||||||
| x | -
|
|
|
|
| ||||||||||
| f(x) | 0 |
|
0 | -
|
0 |
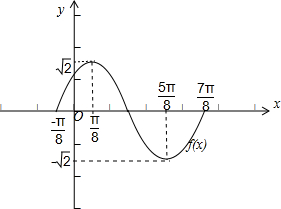
(3)∵g(x)=
| 2a |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3 |
| 4 |
∴-1≤
| 2 |
| π |
| 4 |
| 2 |
| 2 |
| π |
| 4 |
| 2 |
或a<0,
| 2 |
| 2 |
| π |
| 4 |
∴
| 2 |
| 2 |
点评:本题主要考查三角函数的恒等变换,用五点法作函数y=Asin(ωx+φ)在一个周期上的简图,正弦函数的定义域和值域,属于中档题.

练习册系列答案
相关题目