题目内容
直线l:y=x-1与抛物线C:y2=2px(p>0)相交于A,B两点,且直线l过C的焦点.
(1)求抛物线C的方程.
(2)若以AB为直径作圆Q,求圆Q的方程.
解:(1)∵直线l:y=x-1过C的焦点F(
 ,0),∴0=
,0),∴0=
 -1,解得p=2,∴抛物线C的方程为y2=4x.
-1,解得p=2,∴抛物线C的方程为y2=4x.
(2)联立解方程组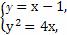
 消去y得x2-6x+1=0,设A(x1,y1),B(x2,y2),则x1+x2=6,x1x2=1,
消去y得x2-6x+1=0,设A(x1,y1),B(x2,y2),则x1+x2=6,x1x2=1,
y1+y2=(x1-1)+(x2-1)=(x1+x2)-2=6-2=4,∴圆Q的圆心Q(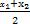
 ,
,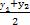
 ),即Q(3,2),
),即Q(3,2),
半径r=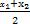
 +
+
 =
=
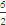 +
+
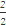 =4,∴圆Q的方程为(x-3)2+(y-2)2=16.
=4,∴圆Q的方程为(x-3)2+(y-2)2=16.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 = .
= . 的图象在点
的图象在点 处的切线方程是
处的切线方程是 ,则
,则 _______________.
_______________. +
+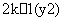 =1表示焦点在y轴上的椭圆,则实数k的取值范围( )
=1表示焦点在y轴上的椭圆,则实数k的取值范围( ) B.(1,+∞) C.(1,2) D.
B.(1,+∞) C.(1,2) D.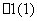
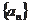 的公比为正数,且a3·a9=2·a52
的公比为正数,且a3·a9=2·a52 ,a2=1则a1= 。
,a2=1则a1= 。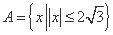 ,
,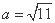 ,则( )
,则( )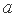
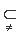
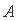 B.
B.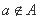 C.
C.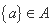 D.
D.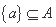
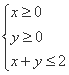 ,则z=4x+y的最大值为( )
,则z=4x+y的最大值为( ) ,则
,则 等于( )
等于( )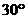 B.
B. C.
C. D.
D.
 是复数
是复数 为纯虚数的( )
为纯虚数的( )