题目内容
已知a,b,c,d都是实数，且a2+b2=r2,c2+d2=R2,求证|ac+bd|≤
(r＞0,R＞0).
证法一：（综合法）∵a、b、c、d都是实数， ∴|ac+bd|≤|ac|+|bd|≤ ∵a2+b2=r2,c2+d2=R2,∴|ac+bd|≤ 证法二：（比较法）显然|ac+bd|≤ 先证ac+bd≤ ac+bd- ∴ac+bd≤ 再证ac+bd≥- ac+bd+ ∴ac+bd≥- 综上，|ac+bd|≤ 证法三：（分析法）要证明|ac+bd|≤ 只要证明（ac+bd）2≤( ∵a2c2≤ ∴a2c2+2abcd+b2d2≤ ∴|ac+bd|≤ 这三种证法说明了证明不等式的方法是多种多样的，我们根据不等式的特点选择适当的证法.一般地说，如果能用分析法寻找出证明某个不等式的途径，那么就能用综合法证明不等式，同时还能启发我们是否能用比较法来证明.+
=
.
.
-
（r2+R2）≤ac+bd≤
(r2+R2).
(r2+R2).
(r2+R2)=ac+bd-
=-
［(a-c)2+(b-d)2］≤0.
(r2+R2).
(r2+R2).
(r2+R2)=ac+bd+
(a2+b2+c2+d2)=
［(a+c)2+(b+d)2］≥0.
(r2+R2).
.
成立，
)2，只要证明a2c2+2abcd+b2d2≤
［(a2+c2)2+2(a2+c2)(b2+d2)+(b2+d2)2］.
(a2+c2)2,2abcd≤
,b2d2≤
(b2+d2)2.
［(a2+c2)2+2(a2+c2)（b2+d2）+(b2+d2)2］成立.
.
1加1阅读好卷系列答案
专项复习训练系列答案
初中语文教与学阅读系列答案
完形填空与阅读理解周秘计划系列答案
英语阅读理解150篇系列答案
奔腾英语系列答案
标准阅读系列答案
53English系列答案
考纲强化阅读系列答案
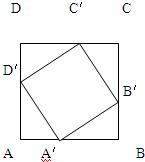已知ABCD，A'B'C'D'都是正方形（如图），而A'、B'、C'、D'分别把AB、BC、CD、DA分为m：n，设AB=1．
.m是两条不重合的直线，则α∥β的一个充分而不必要条件是