Question

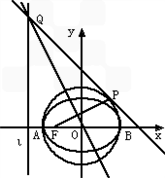
已知：如图，圆O：x²+y²=2交x轴于A，B两点，曲线C是以AB为长轴，离心率为

2

2

的椭圆，其左焦点为F，若P是圆O上一点，连接PF，过原点O作直线PF的垂线交椭圆的左准线l于点Q．
（1）求椭圆的标准方程；
（2）若点P的坐标为（1，1），
①求线段PQ的长；
②求证：直线PQ与圆O相切．

Answer 1

分析：（1）因为a=

2

，e=

2

2

，所以c=1，由此能得到椭圆C的标准方程；
（2）①根据过原点O作直线PF的垂线交椭圆的左准线l于点Q，可求Q的坐标，从而可求线段PQ的长；
②直线PQ的方程为：y=-（x-1）+1，即x+y-2=0，利用点O到直线PQ的距离，可证直线PQ与圆O相切．

解答：（1）解：设椭圆C的标准方程为

x2

a2

+

y2

b2

=1(a＞b＞0)
因为圆O：x²+y²=2交x轴于A，B两点，所以|AB|=2

2

∵曲线C是以AB为长轴，∴2a=2

2

，∴a=

2

∵椭圆的离心率为

2

2

，
∴c=1，
∴b=

a2-c2

=1
∴此椭圆的标准方程为

x2

2

+y2=1
（2）①解：由（1）知椭圆的左焦点F（-1，0），而点P（1，1）
所以直线PF的方程为

y-0

1-0

=

x+1

1+1

，即y=

1

2

(x+1)
直线QO的方程为y=-2x，而椭圆的左准线方程为x=-2，所以点Q的坐标为（-2，4）
因此|PQ|=3

2

②证明：直线PQ的方程为：y=-（x-1）+1，即x+y-2=0
而点O到直线PQ的距离为d=

2

2

=

2

=r
所以直线PQ与圆O相切

点评：本题重点考查椭圆的标准方程，考查直线与圆的位置关系，解题时要认真审题，合理运用椭圆的几何性质．