题目内容

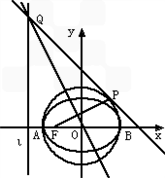
已知：如图，圆O：x²+y²=2交x轴于A，B两点，曲线C是以AB为长轴，离心率为

的椭圆，其左焦点为F，若P是圆O上一点，连接PF，过原点O作直线PF的垂线交椭圆的左准线l于点Q．
（1）求椭圆的标准方程；
（2）若点P的坐标为（1，1），①求线段PQ的长；②求证：直线PQ与圆O相切．

（1）解：设椭圆C的标准方程为

因为圆O：x²+y²=2交x轴于A，B两点，
所以|AB|=2

∵曲线C是以AB为长轴，
∴

，
∴

∵椭圆的离心率为

，
∴c=1，
∴

∴此椭圆的标准方程为

（2）①解：由（1）知椭圆的左焦点F（﹣1，0），而点P（1，1）
所以直线PF的方程为

，即

直线QO的方程为y=﹣2x，而椭圆的左准线方程为x=﹣2，
所以点Q的坐标为（﹣2，4）
因此|PQ|=3

②证明：直线PQ的方程为：y=﹣（x﹣1）+1，即x+y﹣2=0
而点O到直线PQ的距离为d=

所以直线PQ与圆O相切

练习册系列答案

一线名师提优试卷系列答案

一路领先优选卷系列答案

一路领先口算题卡系列答案

一课3练课时导练系列答案

一飞冲天课时作业系列答案

一本到位系列答案

阳光试卷单元测试卷系列答案

阳光课堂星球地图出版社系列答案

训练与检测系列答案

学在荆州系列答案

相关题目

如图，已知△ABC内接于圆O，AB是圆O的直径，四边形DCBE为平行四边形，DC⊥平面ABC，AB=2，tan∠EAB=

．
（1）证明：平面ACD⊥平面ADE；
（2）记AC=x，V（x）表示三棱锥A-CBE的体积，求V（x）的表达式．

已知：如图，圆O：x²+y²=2交x轴于A，B两点，曲线C是以AB为长轴，离心率为

的椭圆，其左焦点为F，若P是圆O上一点，连接PF，过原点O作直线PF的垂线交椭圆的左准线l于点Q．
（1）求椭圆的标准方程；
（2）若点P的坐标为（1，1），
①求线段PQ的长；
②求证：直线PQ与圆O相切．

[选做题]在A、B、C、D四小题中只能选做2题，每小题10分，计20分．请把答案写在答题纸的指定区域内．
A．（选修4-1：几何证明选讲）
如图，圆O的直径AB=8，C为圆周上一点，BC=4，过C作圆的切线l，过A作直线l的垂线AD，D为垂足，AD与圆O交于点E，求线段AE的长．
B．（选修4-2：矩阵与变换）
已知二阶矩阵A有特征值λ₁=3及其对应的一个特征向量α1=

，特征值λ₂=-1及其对应的一个特征向量α2=

，求矩阵A的逆矩阵A^-1．
C．（选修4-4：坐标系与参数方程）
以平面直角坐标系的原点O为极点，x轴的正半轴为极轴，建立极坐标系（两种坐标系中取相同的单位长度），已知点A的直角坐标为（-2，6），点B的极坐标为(4，

)，直线l过点A且倾斜角为

，圆C以点B为圆心，4为半径，试求直线l的参数方程和圆C的极坐标方程．
D．（选修4-5：不等式选讲）
设a，b，c，d都是正数，且x=

．求证：xy≥

已知：如图，圆O：x²+y²=2交x轴于A，B两点，曲线C是以AB为长轴，离心率为 $数学公式$ 的椭圆，其左焦点为F，若P是圆O上一点，连接PF，过原点O作直线PF的垂线交椭圆的左准线l于点Q．
（1）求椭圆的标准方程；
（2）若点P的坐标为（1，1），
①求线段PQ的长；
②求证：直线PQ与圆O相切．