题目内容
2.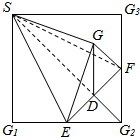 如图,在正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,D是EF的中点,现沿SE,SF及EF把这个正方形折成一个几何体,使G1,G2,G3三点重合于点G,这样,下列五个结论:①SG⊥平面EFG;②SD⊥平面EFG;③GF⊥平面SEF;④EF⊥平面GSD;⑤GD⊥平面SEF.
如图,在正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,D是EF的中点,现沿SE,SF及EF把这个正方形折成一个几何体,使G1,G2,G3三点重合于点G,这样,下列五个结论:①SG⊥平面EFG;②SD⊥平面EFG;③GF⊥平面SEF;④EF⊥平面GSD;⑤GD⊥平面SEF.其中正确的是①(填序号).
分析 根据题意,在折叠过程中,始终有SG1⊥G1E,SG3⊥G3F,即SG⊥GE,SG⊥GF,由线面垂直的判定定理,易得SG⊥平面EFG,分析四各个选项,即可给出正确的选择.
解答 证明:∵在折叠过程中,始终有SG1⊥G1E,SG3⊥G3F,
即SG⊥GE,SG⊥GF,
∴SG⊥平面EFG.
故答案为:①.
点评 本题主要考查了垂直问题的证明,其一般规律是“由已知想性质,由求证想判定”,也就是说,根据已知条件去思考有关的性质定理;根据要求证的结论去思考有关的判定定理,往往需要将分析与综合的思路结合起来.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
13.下列函数中,在(0,+∞)上是减函数的是( )
| A. | y=$\sqrt{x}$ | B. | y=lnx | C. | y=$\frac{1}{x}$ | D. | y=2x |
7.若函数f(x)=|2x-2|-b有两个零点,则实数b的取值范围是( )
| A. | (-∞,0) | B. | (0,1) | C. | (0,2) | D. | (2,+∞) |
11.已知x,y取值如表:
画散点图可知:y与x线性相关,且求得回归线方程为$\widehat{y}$=$\widehat{x}$+1,则m的值为1.7(精确到0.1)
| x | 0 | 1 | 4 | 5 | 6 |
| y | 1.3 | m | 3m | 5.6 | 7.4 |