题目内容
已知函数
 ,f '(x)为f(x)的导函数,若f '(x)是偶函数且f '(1)=0.
,f '(x)为f(x)的导函数,若f '(x)是偶函数且f '(1)=0.
⑴求函数 的解析式;
的解析式;
⑵若对于区间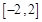 上任意两个自变量的值
上任意两个自变量的值 ,都有
,都有 ,求实数
,求实数 的最小值;
的最小值;
⑶若过点
 ,可作曲线
,可作曲线 的三条切线,求实数
的三条切线,求实数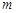 的取值范围.
的取值范围.
⑴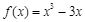 ;⑵
;⑵ 的最小值为
的最小值为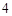 ;⑶
;⑶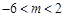 .
.
解析试题分析:⑴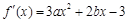 ,由
,由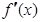 是偶函数得
是偶函数得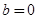 .又
.又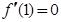 ,所以
,所以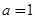 ,由此可得解析式;
,由此可得解析式;
⑵对于区间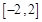 上任意两个自变量的值
上任意两个自变量的值 ,都有
,都有 ,则只需
,则只需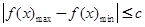 即可.所以接下来就利用导数求
即可.所以接下来就利用导数求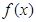 在区间
在区间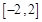 上的最大值与最小值,然后代入
上的最大值与最小值,然后代入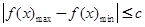 解不等式即可得
解不等式即可得 的最小值.⑶易知点
的最小值.⑶易知点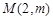
 不在曲线
不在曲线 上.凡是过某点的切线(不是在某点处的切线)的问题,都要设出切点坐标然后列方程组..
上.凡是过某点的切线(不是在某点处的切线)的问题,都要设出切点坐标然后列方程组..
设切点为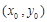 .则
.则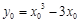 .又
.又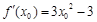 ,∴切线的斜率为
,∴切线的斜率为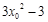 .
.
由此得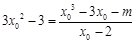 ,即
,即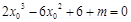 .下面就考查这个方程的解的个数.
.下面就考查这个方程的解的个数.
因为过点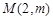
 ,可作曲线
,可作曲线 的三条切线,所以方程
的三条切线,所以方程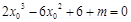 有三个不同的实数解.即函数
有三个不同的实数解.即函数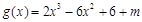 有三个不同的零点.接下来就利用导数结合图象研究这个函数的零点的个数.
有三个不同的零点.接下来就利用导数结合图象研究这个函数的零点的个数.
试题解析:⑴∵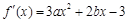 ,1分
,1分
由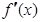 是偶函数得
是偶函数得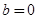 .又
.又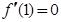 ,所以
,所以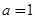 3分
3分
∴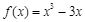 .4分
.4分
⑵令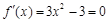 ,即
,即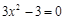 ,解得
,解得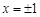 .5分
.5分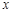
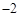
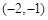
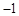
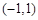
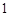
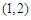
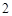
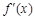
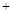



新路学业寒假作业快乐假期新疆青少年出版社系列答案
新课堂假期生活假期作业寒假合编系列答案
新课程寒假作业广西师范大学出版社系列答案
新课程寒假作业本系列答案
新课标快乐提优寒假作业陕西旅游出版社系列答案
新课标寒假衔接系列答案
新课标高中假期作业系列答案
新课标高中寒假作业合肥工业大学出版社系列答案
石室金匮寒假作业系列答案
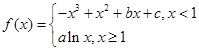 的图像过坐标原点
的图像过坐标原点 ,且在点
,且在点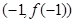 处的切线斜率为
处的切线斜率为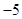 .
.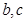 的值;
的值; 在区间
在区间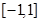 上的最小值;
上的最小值;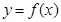 的图像上存在两点
的图像上存在两点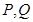 ,使得对于任意给定的正实数
,使得对于任意给定的正实数 都满足
都满足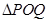 是以
是以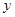 轴上,求点
轴上,求点 的横坐标的取值范围.
的横坐标的取值范围.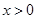 ,函数
,函数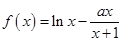 .
.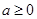 时,讨论函数
时,讨论函数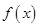 的单调性;
的单调性;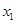 和
和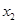 )时,求证:
)时,求证: .
.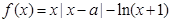 .
. 时,求函数
时,求函数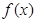 的单调区间;
的单调区间;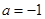 时,若
时,若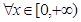 ,
,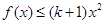 恒成立,求实数
恒成立,求实数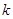 的最小值;
的最小值;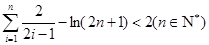 .
.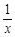 -(2+a)lnx(a≥0)
-(2+a)lnx(a≥0) 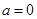 时,求
时,求 的极值;
的极值;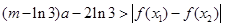 成立,求实数m的取值范围。
成立,求实数m的取值范围。 R
R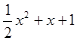 有唯一公共点;
有唯一公共点;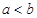 ,比较
,比较 与
与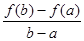 的大小,并说明理由。
的大小,并说明理由。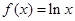 ,
,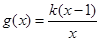 .
.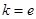 时,求函数
时,求函数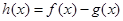 的单调区间和极值;
的单调区间和极值;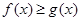 恒成立,求实数
恒成立,求实数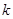 的值.
的值. 。
。 时,函数
时,函数 取得极值,求函数
取得极值,求函数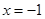 处的切线方程;
处的切线方程;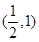 内不单调,求实数
内不单调,求实数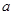 的取值范围。
的取值范围。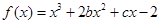 的图象在与
的图象在与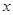 轴交点处的切线方程是
轴交点处的切线方程是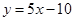 .
. 的解析式;
的解析式;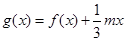 ,若
,若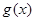 的极值存在,求实数
的极值存在,求实数 的取值范围以及函数
的取值范围以及函数