题目内容
用二项式定理证明:32n+2-8n-9是64的倍数(n∈N).
分析:①变为二项式形式;②与64联系上.
证明:32n+2-8n-9=9n+1-8(n+1)-1=(8+1)n+1-8(n+1)-1=8n+1+C![]() 8n+C
8n+C![]() 8n-1+…+C
8n-1+…+C![]() 82+
82+![]() +
+![]() 8+
8+
C![]() -8(n+1)-1=82(8n-1+C
-8(n+1)-1=82(8n-1+C![]() +18n-2+…+C
+18n-2+…+C![]() ).
).
∵括号内每一项都是自然数,和为自然数,
∴上式是64的倍数,即32n+2-8n-9是64的倍数.
绿色通道:利用二项式定理可以求余数和证明整除性问题,通常需将底数化成两数的和与差的形式,且这种转化形式与除数有密切的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
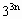 -26n-1能被676整除;
-26n-1能被676整除;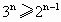 (n+2)(n∈N);
(n+2)(n∈N);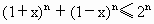 .
.