题目内容
如图,四棱锥 的底面是边长为1的正方形,
的底面是边长为1的正方形, ,点E在棱PB上.
,点E在棱PB上.
(1)求证:平面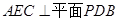 ;
;
(2)当 且E为PB的中点时,求AE与平面PDB
且E为PB的中点时,求AE与平面PDB
所成的角的大小.
(1)见解析(2)
解析试题分析:(1)利用面面垂直的判定定理证明;(2)利用直线与平面所成的角的定义求解
试题解析:(1)∵四边形ABCD是正方形, ,
,
∵ ,
,
∴ ,
,
∴平面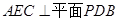 .
.
(2)设 ,连接OE,
,连接OE,
由(1)知 于O,
于O,
∴∠AEO为AE与平面PDB所的角,
∴O,E分别为DB、PB的中点,
∴OE//PD, ,又∵
,又∵ ,
,
∴OE⊥底面ABCD,OE⊥AO,
在Rt△AOE中, ,
,
∴ ,即AE与平面PDB所成的角的大小为
,即AE与平面PDB所成的角的大小为 .
.
考点:面面垂直的判定定理

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中, 底面
底面 ,
,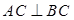 ,
, 为
为 的中点,
的中点,  为
为 的中点,
的中点, ,
, .
.
 平面
平面 ;
; 与平面
与平面 成角的正弦值;
成角的正弦值; 在线段
在线段 上,且
上,且 ,
, 平面
平面 ,求实数
,求实数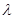 的值.
的值. 为正方形,四边形
为正方形,四边形 是直角梯形,
是直角梯形, ,
, 平面
平面 .
.
 平面
平面 ;
; 与平面
与平面 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, 平面
平面 ,
, ,
, ,
, .
.
 平面
平面 ;
; 与平面
与平面 所成角的正切值.
所成角的正切值.
 AB.Q是PC上的一点.
AB.Q是PC上的一点.
 的底面是边长为2的正三角形,且侧棱垂直于底面,侧棱长是,D是AC的中点。
的底面是边长为2的正三角形,且侧棱垂直于底面,侧棱长是,D是AC的中点。
 平面
平面 ;
; 的大小;
的大小; 与平面
与平面