题目内容
已知双曲线的方程为4x2-9y2=36，求双曲线的顶点坐标，焦点坐标，离心率，准线方程，渐近线方程．
解：将方程化为标准方程得：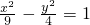
∴a=3，b=2，
∴c2=a2+b2=13
∴
∴顶点坐标：（±3，0），焦点坐标：（±
，0），离心率：
，
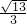准线方程x=±
，渐近线方程：y=±
x．
分析：将双曲线方程化为标准方程，求得a，b，c，从而可求双曲线的几何性质．
点评：本题以双曲线方程为载体，考查双曲线的标准方程，考查双曲线的几何性质，属于基础题．
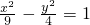
∴a=3，b=2，
∴c2=a2+b2=13
∴
∴顶点坐标：（±3，0），焦点坐标：（±
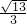，0），离心率：，准线方程x=±
，渐近线方程：y=±x．分析：将双曲线方程化为标准方程，求得a，b，c，从而可求双曲线的几何性质．
点评：本题以双曲线方程为载体，考查双曲线的标准方程，考查双曲线的几何性质，属于基础题．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
-
=1,过其右焦点作一条垂直于x轴的直线与此双曲线交于A、B两点,则|AB|的长为（ ）
-
=1,过其右焦点作一条垂直于x轴的直线与此双曲线交于A、B两点,则|AB|的长为（ ）
，则它的一个焦点到一条渐进线的距离是（ ）
D. 12
的焦距为4，以原点为圆心，实半轴长为半径的圆和直线
相切．
为定值？若存在，求出此定值和所有的定点M的坐标；若不存在，请说明理由．