题目内容
已知双曲线 的焦距为4,以原点为圆心,实半轴长为半径的圆和直线
的焦距为4,以原点为圆心,实半轴长为半径的圆和直线 相切.
相切.(Ⅰ) 求双曲线E的方程;
(Ⅱ)已知点F为双曲线E的左焦点,试问在x轴上是否存在一定点M,过点M任意作一条直线l交双曲线E于P,Q两点,使
 为定值?若存在,求出此定值和所有的定点M的坐标;若不存在,请说明理由.
为定值?若存在,求出此定值和所有的定点M的坐标;若不存在,请说明理由.
【答案】分析:(I)利用点到直线的距离公式求得a,再根据焦距,求得b.
(II)假设存在满足条件的点M,先在直线垂直于y轴时,求得定值,再结合韦达定理根与系数的关系,分析验证直线不垂直于y轴时,求得此定值的情况,从而得出结论.
解答:解:(Ⅰ)原点到直线 x-y+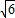 =0的距离d=
=0的距离d= =
=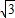 ,
,
∴ ,∴b=1,
,∴b=1,
∴双曲线E的方程为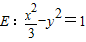 ;
;
(Ⅱ)解法一:假设存在点M(m,0)满足条件,
①当直线l方程为y=0时,则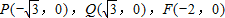 ,∴
,∴ ;
;
②当直线l方程不是y=0时,可设直线l:x=ty+m,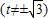 代入
代入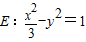
整理得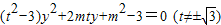 ,*
,*
由△>0得m2+t2>9,
设方程*的两个根为y1,y2,满足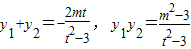 ,∴
,∴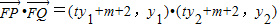 =
=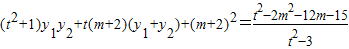 ,
,
当且仅当2m2+12m+15=3时,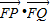 为定值1,
为定值1,
解得 ,
,
∵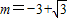 不满足对任意t≠±
不满足对任意t≠± ,△>0,∴不合题意,舍去.
,△>0,∴不合题意,舍去.
而且 满足△>0;
满足△>0;
综上得:过定点 任意作一条直线l交双曲线E于P,Q两点,使
任意作一条直线l交双曲线E于P,Q两点,使 为定值1.
为定值1.
解法二:前同解法一,得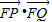 =
=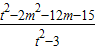 ,
,
由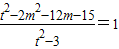 ⇒2m2+12m+15=3,
⇒2m2+12m+15=3,
解得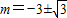 ,下同解法一.
,下同解法一.
解法三:当直线l不垂直x轴时,设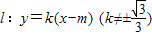 ,代入
,代入
整理得 ,*
,*
由△>0得m2k2-3k2+1>0,
设方程*的两个根为x1,x2,满足 ,
,
∴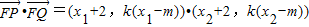 =
=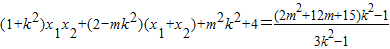 ,
,
当且仅当2m2+12m+15=3时,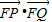 为定值1,
为定值1,
解得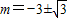 ,
,
∵不满足对任意K≠±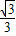 ,△>0,∴
,△>0,∴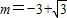 不合题意,舍去,
不合题意,舍去,
而且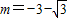 满足△>0;
满足△>0;
当直线l⊥x轴时, 代入
代入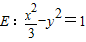 得
得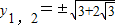 ,
,
∴ ;…(9分)
;…(9分)
综上得:(结论同解法一)
点评:本题借助存在性问题考查圆锥曲线中的定值问题.本题的解答是解决存在性问题的一般思路,巧妙的利用韦达定理根与系数的关系分析求解是关键.
另:第(II)题有一般性结论
(II)假设存在满足条件的点M,先在直线垂直于y轴时,求得定值,再结合韦达定理根与系数的关系,分析验证直线不垂直于y轴时,求得此定值的情况,从而得出结论.
解答:解:(Ⅰ)原点到直线 x-y+
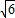 =0的距离d=
=0的距离d= =
=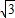 ,
,∴
 ,∴b=1,
,∴b=1,∴双曲线E的方程为
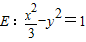 ;
; (Ⅱ)解法一:假设存在点M(m,0)满足条件,
①当直线l方程为y=0时,则
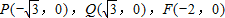 ,∴
,∴ ;
;②当直线l方程不是y=0时,可设直线l:x=ty+m,
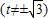 代入
代入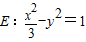
整理得
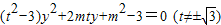 ,*
,*由△>0得m2+t2>9,
设方程*的两个根为y1,y2,满足
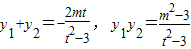 ,∴
,∴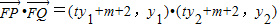 =
=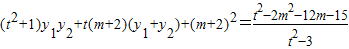 ,
,当且仅当2m2+12m+15=3时,
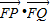 为定值1,
为定值1,解得
 ,
,∵
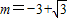 不满足对任意t≠±
不满足对任意t≠± ,△>0,∴不合题意,舍去.
,△>0,∴不合题意,舍去.而且
 满足△>0;
满足△>0;综上得:过定点
 任意作一条直线l交双曲线E于P,Q两点,使
任意作一条直线l交双曲线E于P,Q两点,使 为定值1.
为定值1.解法二:前同解法一,得
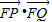 =
=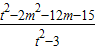 ,
,由
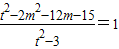 ⇒2m2+12m+15=3,
⇒2m2+12m+15=3,解得
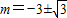 ,下同解法一.
,下同解法一.解法三:当直线l不垂直x轴时,设
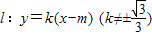 ,代入
,代入
整理得
 ,*
,*由△>0得m2k2-3k2+1>0,
设方程*的两个根为x1,x2,满足
 ,
,∴
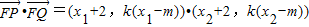 =
=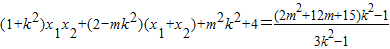 ,
,当且仅当2m2+12m+15=3时,
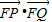 为定值1,
为定值1,解得
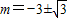 ,
,∵不满足对任意K≠±
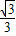 ,△>0,∴
,△>0,∴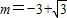 不合题意,舍去,
不合题意,舍去,而且
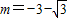 满足△>0;
满足△>0; 当直线l⊥x轴时,
 代入
代入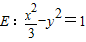 得
得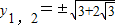 ,
,∴
 ;…(9分)
;…(9分)综上得:(结论同解法一)
点评:本题借助存在性问题考查圆锥曲线中的定值问题.本题的解答是解决存在性问题的一般思路,巧妙的利用韦达定理根与系数的关系分析求解是关键.
另:第(II)题有一般性结论

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
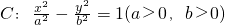 的焦距为4,且过点(2,3),则它的渐近线方程为________.
的焦距为4,且过点(2,3),则它的渐近线方程为________. y=0和x+
y=0和x+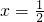
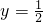
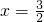
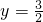
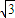 y=0和x+
y=0和x+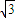 y=0,双曲线上的点满足不等式x2-3y2<0,已知双曲线的焦距为4,则双曲线的准线方程为( )
y=0,双曲线上的点满足不等式x2-3y2<0,已知双曲线的焦距为4,则双曲线的准线方程为( )