题目内容
【题目】已知函数![]() (其中
(其中![]() 是自然对数的底数),
是自然对数的底数),![]() .
.
(Ⅰ)求函数![]() 的极值;
的极值;
(Ⅱ)设![]() ,若
,若![]() 满足
满足![]() 且
且![]() ,试判断方程
,试判断方程![]() 的实数根个数,并说明理由.
的实数根个数,并说明理由.
【答案】(Ⅰ)![]() ,但无极小值;(Ⅱ)有2个实数根,利用见解析.
,但无极小值;(Ⅱ)有2个实数根,利用见解析.
【解析】
(I)利用![]() 的导函数
的导函数![]() 研究
研究![]() 的单调性,由此求得
的单调性,由此求得![]() 的极值.
的极值.
(II)求得![]() 的表达式,求得其导函数
的表达式,求得其导函数![]() ,由此求得
,由此求得![]() 的单调区间、极小值(最小值),结合零点存在性定理,判断出
的单调区间、极小值(最小值),结合零点存在性定理,判断出![]() 有两个实数根.
有两个实数根.
(Ⅰ)因为![]() ,所以
,所以![]() .
.
当![]() 时,
时,![]() ,此时
,此时![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,此时
,此时![]() 单调递减.
单调递减.
所以![]() ,但无极小值.
,但无极小值.
(Ⅱ)因为![]() ,所以
,所以
因为![]() ,所以
,所以![]() ,于是
,于是![]() .
.
令![]() ,得
,得![]() 或
或![]() .
.
当![]() 时,
时,![]() ,此时
,此时![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,此时
,此时![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,此时
,此时![]() 单调递增.
单调递增.
所以![]() .
.
因为![]() ,所以
,所以![]() ,
,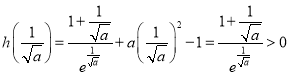 .
.
又函数![]() 在
在![]() 上连续,故
上连续,故![]() 有一个零点为0,且在
有一个零点为0,且在![]() 上也有一个零点.
上也有一个零点.
综上,方程![]() 的有2个实数根.
的有2个实数根.

练习册系列答案
相关题目
【题目】某公司的甲、乙两名工程师因为工作需要,各自选购一台笔记本电脑.该公司提供了![]() 三款笔记本电脑作为备选,这三款笔记本电脑在某电商平台的销量和用户评分如下表所示:
三款笔记本电脑作为备选,这三款笔记本电脑在某电商平台的销量和用户评分如下表所示:
型号 |
|
|
|
销量(台) | 2000 | 2000 | 4000 |
用户评分 | 8 | 6.5 | 9.5 |
若甲选购某款笔记本电脑的概率与对应的销量成正比,乙选购某款笔记本电脑的概率与对应的用户评分减去5的值成正比,且他们两人选购笔记本电脑互不影响.
(1)求甲、乙两人选购不同款笔记本电脑的概率;
(2)若公司给购买这三款笔记本电脑的员工一定的补贴,补贴标准如下表:
型号 |
|
|
|
补贴(千元) | 3 | 4 | 5 |
记甲、乙两人获得的公司补贴之和为![]() 千元,求
千元,求![]() 的分布列和数学期望.
的分布列和数学期望.

