题目内容
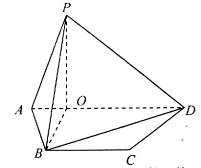
如图,三棱锥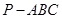 中,
中,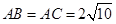 ,
,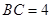 ,
, ,点
,点 在平面
在平面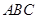 内的射影恰为
内的射影恰为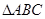 的重心
的重心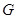 ,M为侧棱
,M为侧棱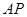 上一动点.
上一动点.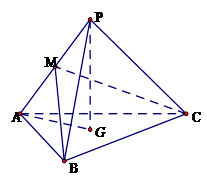
(1)求证:平面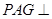 平面
平面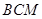 ;
;
(2)当M为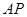 的中点时,求直线
的中点时,求直线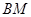 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(1)详见解析;(2) .
.
解析试题分析:(1)证明平面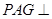 平面
平面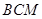 ,证明面面垂直,先证线面垂直,即证一个平面过另一个平面的垂线,本题根据面面垂直的判定定理可知在平面
,证明面面垂直,先证线面垂直,即证一个平面过另一个平面的垂线,本题根据面面垂直的判定定理可知在平面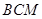 内找一条直线与平面
内找一条直线与平面 垂直,由已知
垂直,由已知 平面
平面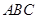 ,可得
,可得 ,由题意可知,
,由题意可知,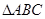 是等腰三角形,且
是等腰三角形,且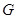 为重心,既得
为重心,既得 ,从而得
,从而得 平面
平面 ,可证平面
,可证平面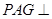 平面
平面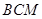 ;(2)当M为
;(2)当M为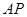 的中点时,求直线
的中点时,求直线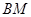 与平面
与平面 所成角的正弦值,求线面角,传统方法是找线和射影所成的角,本题找射影比较麻烦,可用向量法来求,过
所成角的正弦值,求线面角,传统方法是找线和射影所成的角,本题找射影比较麻烦,可用向量法来求,过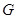 作
作 的平行线为
的平行线为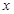 轴,
轴, 为
为 轴,
轴, 为
为 轴建立空间直角坐标系,写出各点的坐标,求出平面
轴建立空间直角坐标系,写出各点的坐标,求出平面 的一个法向量,利用线面角的正弦值等于线和法向量所成角的余弦值即可求出直线
的一个法向量,利用线面角的正弦值等于线和法向量所成角的余弦值即可求出直线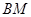 与平面
与平面 所成角的正弦值.
所成角的正弦值.
试题解析:(1)取 中点
中点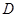 ,连接
,连接 、
、 ,
,
∵ 平面
平面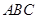 ,∴
,∴
等腰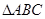 中,
中,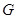 为重心,∴
为重心,∴
∴ 平面
平面
∴平面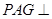 平面
平面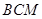 6分
6分
(2)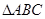 中,
中, ∴
∴
∵ 平面
平面 ∴
∴
∴ ∴
∴
过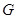 作
作 的平行线为
的平行线为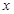 轴,
轴, 为
为 轴,
轴, 为
为 轴
轴
建立空间直角坐标系



∴ 
设直线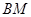 与平面
与平面 所成角为
所成角为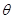
设平面 的法向量为
的法向量为
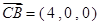
 ∴
∴

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 中,底面
中,底面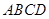 是直角梯形,
是直角梯形, ,
, ,
,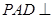 平面
平面
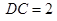 ,
,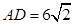 ,
, ,
, ,且
,且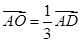 .
.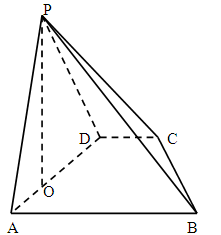
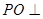 平面
平面 与平面
与平面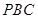 所成二面角的大小为
所成二面角的大小为 ,求
,求 的值.
的值.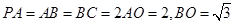 .
.
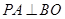 ;
;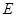 是以
是以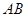 为直径的半圆
为直径的半圆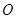 上异于
上异于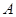 、
、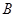 的点,矩形
的点,矩形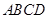 所在的平面垂直于半圆
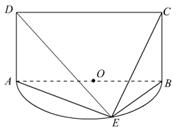
所在的平面垂直于半圆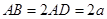 .
.
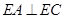 ;
;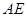 和
和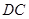 所成的角为
所成的角为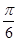 ,求平面
,求平面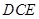 与平面
与平面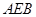 所成的锐二面角的余弦值.
所成的锐二面角的余弦值. 中,
中, 为
为 的中点,
的中点, ,
, ,
, .将此平面四边形
.将此平面四边形 折成直二面角
折成直二面角 ,
,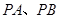 ,设
,设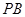 中点为
中点为 .
.
 平面
平面 ;
; 上是否存在一点
上是否存在一点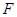 ,使得
,使得 平面
平面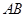 与平面
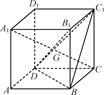
与平面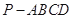 中,侧面
中,侧面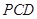
 底面
底面 ,
,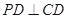 ,底面
,底面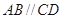 ,
,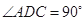 ,
,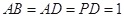 ,
,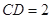 .
.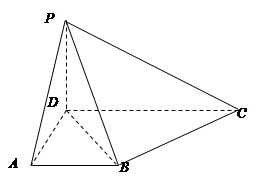
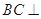 平面
平面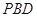 ;
;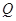 为侧棱
为侧棱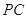 上一点,
上一点,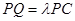 ,试确定
,试确定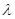 的值,使得二面角
的值,使得二面角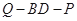 为
为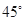 .
.

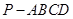 的底面
的底面 为一直角梯形,侧面PAD是等边三角形,其中
为一直角梯形,侧面PAD是等边三角形,其中 ,
,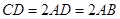 ,平面
,平面 底面
底面 是
是 的中点.
的中点.
 //平面
//平面 ;
; 与平面BDE所成角的余弦值;
与平面BDE所成角的余弦值;