题目内容
函数 单调增区间是________,值域是________.
单调增区间是________,值域是________.
(1,4) [-2,+∞]
分析:本题为复合函数的单调区间和值域问题,复合函数单调区间满足“同增异减”原则,而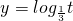 在(0,+∞)上是减函数,所以只需求t=-x2+2x+8的单调递减区间即可,又因为-x2+2x+8在真数位置,故需大于0;求值域时,先求t=-x2+2x+8的范围,再求
在(0,+∞)上是减函数,所以只需求t=-x2+2x+8的单调递减区间即可,又因为-x2+2x+8在真数位置,故需大于0;求值域时,先求t=-x2+2x+8的范围,再求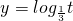 的值域即可.
的值域即可.
解答: 由函数
由函数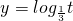 和t=-x2+2x+8复合而成,
和t=-x2+2x+8复合而成,
而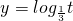 在(0,+∞)上是减函数,
在(0,+∞)上是减函数,
又因为-x2+2x+8在真数位置,
故需大于0,t=-x2+2x+8>0的单调递减区间为(1,4).
t=-x2+2x+8的值域为(0,9],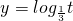 ,t∈(0,9]的值域为[-2,+∞).
,t∈(0,9]的值域为[-2,+∞).
故答案为:(1,4)(或[1,4));[-2,+∞).
点评:本题考查复合函数的单调区间和值域问题,复合函数单调区间满足“同增异减”原则,真数大于0在解题中不要忘掉.
分析:本题为复合函数的单调区间和值域问题,复合函数单调区间满足“同增异减”原则,而
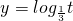 在(0,+∞)上是减函数,所以只需求t=-x2+2x+8的单调递减区间即可,又因为-x2+2x+8在真数位置,故需大于0;求值域时,先求t=-x2+2x+8的范围,再求
在(0,+∞)上是减函数,所以只需求t=-x2+2x+8的单调递减区间即可,又因为-x2+2x+8在真数位置,故需大于0;求值域时,先求t=-x2+2x+8的范围,再求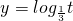 的值域即可.
的值域即可.解答:
 由函数
由函数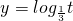 和t=-x2+2x+8复合而成,
和t=-x2+2x+8复合而成,而
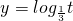 在(0,+∞)上是减函数,
在(0,+∞)上是减函数,又因为-x2+2x+8在真数位置,
故需大于0,t=-x2+2x+8>0的单调递减区间为(1,4).
t=-x2+2x+8的值域为(0,9],
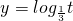 ,t∈(0,9]的值域为[-2,+∞).
,t∈(0,9]的值域为[-2,+∞).故答案为:(1,4)(或[1,4));[-2,+∞).
点评:本题考查复合函数的单调区间和值域问题,复合函数单调区间满足“同增异减”原则,真数大于0在解题中不要忘掉.

练习册系列答案
相关题目
 单调增区间是 ;
单调增区间是 ; 单调增区间是
;
单调增区间是
;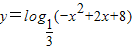 单调增区间是 ,值域是 .
单调增区间是 ,值域是 .