题目内容
古希腊人常用小石子在沙滩上摆成各种形状来研究数。比如:
他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似的,称图2中的1,4,9,16,…这样的数为正方形数。下列数中既是三角形数又是正方形数的是( )
| A.289 | B.1024 | C.1225 | D.1378 |
C
解析试题分析:解:由图形可得三角形数构成的数列通项 an= ,同理可得正方形数构成的数列通项bn=n2,则由bn=n2(n∈N+)可排除D,又由 an=
,同理可得正方形数构成的数列通项bn=n2,则由bn=n2(n∈N+)可排除D,又由 an= ,知an必为奇数,
,知an必为奇数, =289无正整数解,故答案为C
=289无正整数解,故答案为C
考点:归纳猜想思想的运用
点评:考查学生观察、分析和归纳能力,并能根据归纳的结果解决分析问题,注意对数的特性的分析,属中档题

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
已知等比数列 中有
中有 ,数列
,数列 是等差数列,且
是等差数列,且 ,则
,则 ( )
( )
| A.2 | B.4 | C.8 | D.16 |
在等比数列 中,若
中,若 ,则
,则 的值为
的值为
| A.4 | B.2 | C.-2 | D.-4 |
设 ,且
,且 是
是 和
和 的等比中项,则动点
的等比中项,则动点 的轨迹为除去
的轨迹为除去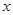 轴上点的( )
轴上点的( )
| A.一条直线 | B.一个圆 | C.一个椭圆 | D.双曲线的一支 |
已知 为等比数列,
为等比数列, ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
已知 为等比数列,
为等比数列, ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
设等比数列 的公比
的公比 , 前n项和为
, 前n项和为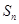 ,则
,则 ( )
( )
| A.2 | B.4 | C. | D. |
已知正项等比数列 满足:
满足: ,若存在两项
,若存在两项 使得
使得 ,则
,则 的最小值为( )
的最小值为( )
A. | B. | C. | D.不存在 |
在各项均为正数的等比数列 中,若
中,若 ,则
,则 =
=
| A.12 | B.10 | C.15 | D. |