题目内容
已知正项等比数列 满足:
满足: ,若存在两项
,若存在两项 使得
使得 ,则
,则 的最小值为( )
的最小值为( )
A. | B. | C. | D.不存在 |
A
解析试题分析:根据题意,正项等比数列 满足:
满足: ,故可知
,故可知 ,那么由于存在两项
,那么由于存在两项 使得
使得 ,则可知
,则可知 ,那么可知
,那么可知 ,故选A.
,故选A.
考点:考查了等比数列的性质,以及不等式知识 。
点评:解决该试题的冠军艾女士对于等比中项的理解运用 ,和均值不等式的运用,一正二定三相等,来求最值,属于中档题。

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
已知等比数列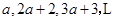 ,则第四项为( )
,则第四项为( )
A.-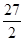 | B.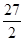 | C.-27 | D.27 |
古希腊人常用小石子在沙滩上摆成各种形状来研究数。比如:
他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似的,称图2中的1,4,9,16,…这样的数为正方形数。下列数中既是三角形数又是正方形数的是( )
| A.289 | B.1024 | C.1225 | D.1378 |
设等比数列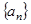 中,前n项和为
中,前n项和为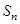 ,已知
,已知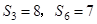 ,则
,则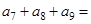
A. | B.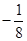 | C.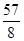 | D.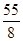 |
数列 为等比数列,
为等比数列, 为其前
为其前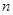 项和,已知
项和,已知 ,则公比
,则公比
A. | B. | C. 或 或 | D. 或 或 |
设等比数列 中,前n项和为
中,前n项和为 ,已知
,已知 ,则
,则 ( )
( )
A. | B. | C. | D. |
已知 是等比数列,
是等比数列, ,则公比
,则公比 =( )
=( )
A. | B. | C.2 | D. |
 中,每 行 中 的 三 个 数 成 等 差 数 列,且
中,每 行 中 的 三 个 数 成 等 差 数 列,且 、
、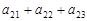 、
、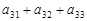 成等比数列,下列四个判断正确的有 (A )
成等比数列,下列四个判断正确的有 (A )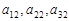 必成等比数列 ②第1列
必成等比数列 ②第1列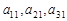 不一定成等比数列
不一定成等比数列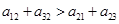 ④若9个数之和等于9,则
④若9个数之和等于9,则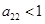
 的左右焦点分别为
的左右焦点分别为 ,P是椭圆上的一点,且
,P是椭圆上的一点,且 成等比数列,则椭圆的离心率的取值范围为( )
成等比数列,则椭圆的离心率的取值范围为( )


