题目内容
已知复数z1=-2i(1+i).
(1)求|z1 |;
|;
(2)若|z|=1,求|z-z1|的最大值.
解:(1)∵z1=-2i(1+i)=2-2i,
∴|z1|= =2
=2 .
.

(2)如图所示,由|z|=1可知,z在复平面内对应的点的轨迹是半径为1,圆心为O(0,0)的圆,而z1对应着坐标系中的点 Z1(2,-2).所以|z-z1|的最大值可以看成是点Z1(2,-2)到圆上的点的距离的最大值.由图知|z-z1|max=|z1|+r(r为圆半径)=2
Z1(2,-2).所以|z-z1|的最大值可以看成是点Z1(2,-2)到圆上的点的距离的最大值.由图知|z-z1|max=|z1|+r(r为圆半径)=2 +1.
+1.

练习册系列答案
相关题目
 轴对称,它的顶点在坐标原点
轴对称,它的顶点在坐标原点 ,并且经过点
,并且经过点 。若点
。若点 到
到 该抛物线焦点的距离为
该抛物线焦点的距离为 ,则
,则 ( )
( ) B、
B、 C、
C、 D、
D、
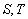 是
是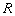 的两个非空子集,如果存在一个从
的两个非空子集,如果存在一个从 到
到 的函数
的函数 满足:
满足:
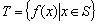 ;
;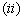 对任意
对任意 ,当
,当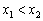 时,恒有
时,恒有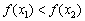 ,那么称这两个集
,那么称这两个集 合“保序同构”,以下集合对不是“保序同构”的是( )
合“保序同构”,以下集合对不是“保序同构”的是( )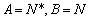 B.
B. 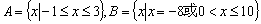
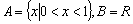 D.
D. 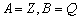
 =( )
=( ) +6x +13 =0的
+6x +13 =0的 一个根是( )
一个根是( ) 上单调递减的函数为
上单调递减的函数为 B.
B. C.
C. D.
D.
 ,若直线
,若直线 与直线
与直线 垂直,则实数
垂直,则实数 .
.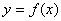 的导函数
的导函数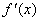 的图象,则下面判断正确的是( ).
的图象,则下面判断正确的是( ).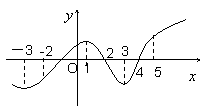 A.函数
A.函数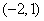 上单调递增
上单调递增 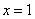 处取得极大值
处取得极大值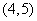 上单调递增
上单调递增 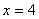 时,
时,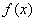 取极大值
取极大值