题目内容
|x+2|+|x﹣3|的取值范围是 .40、函数 的单调递减区间是
的单调递减区间是
解:令f(x)=|x+2|+|x﹣3|= ∵x≥3,2x﹣1≥5;x≤﹣2时,﹣2x+1≥5根据分段函数的性质 可知,f(x)的取值范围f(x)≥5故答案为:[5,+∞)40、
∵x≥3,2x﹣1≥5;x≤﹣2时,﹣2x+1≥5根据分段函数的性质 可知,f(x)的取值范围f(x)≥5故答案为:[5,+∞)40、

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
定义在R上的偶函数f(x)满足f(2﹣x)=f(x),且在[﹣3,﹣2]上是减函数,α,β是钝角三角形的两个锐角,则下列结论正确的是( )
|
| A. | f(sinα)>f(cosβ) | B. | f(cosα)<f(cosβ) | C. | f(cosα)>f(cosβ) | D. | f(sinα)<f(cosβ) |
 中,如果存在常数
中,如果存在常数
 ,使得
,使得 对于任意正整数
对于任意正整数 均成立,那么就称数列
均成立,那么就称数列 的周期. 已知周期数列
的周期. 已知周期数列 满足
满足 ,若
,若 ,当数列
,当数列 时,则数列
时,则数列 为( )
为( ) 内一点(5,3),有一组弦的长度组成等差数列,最小弦长为该数列的首项
内一点(5,3),有一组弦的长度组成等差数列,最小弦长为该数列的首项 ,最大弦长为数列的末项
,最大弦长为数列的末项 ,则
,则 的值是( )A、10 B、 18 C、45 D、54
的值是( )A、10 B、 18 C、45 D、54 ,若对任意
,若对任意 ,恒有
,恒有 成立,不等式
成立,不等式 的解集为
的解集为 ,(Ⅰ)求集合
,(Ⅰ)求集合 ,若集合
,若集合 是集合
是集合 的取值范围。
的取值范围。



 上的函数
上的函数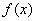 满足
满足 ,则
,则 的值为
的值为 (B)
(B)  (C)
(C)  (D)
(D) 
 ,有下列命题:
,有下列命题: 轴对称;②当
轴对称;②当 时,
时, 是增函数;当
是增函数;当 时,
时, ;
;