题目内容
设 ,
, 是两个非零向量,如果(
是两个非零向量,如果( +3
+3 )⊥(7
)⊥(7 -5
-5 ),且(
),且( -4
-4 )⊥(7
)⊥(7 -2
-2 ),则
),则 与
与 的夹角为 .
的夹角为 .
【答案】分析:由已知可得: ,并且
,并且  ,整理可得
,整理可得  ,将
,将  代回原式可得
代回原式可得  ,即可得到
,即可得到 ,即
,即 ,再
,再
根据向量的夹角公式可求答案.
解答:解:因为 ,
,
所以 ,
,
因为 ,
,
所以 ,
,
两式相减得 ,
,
所以 ,
,
将 代回第一个式子可得:
代回第一个式子可得: ,
,
所以 ,即
,即 .
.
设向量 与
与  的夹角为θ,则
的夹角为θ,则  =
= ,
,
所以向量 与
与  的夹角大小为
的夹角大小为 .
.
故答案为: .
.
点评:本题主要考查了平面向量的数量积的性质:若 ?
? 的应用,即若知道向量垂直,则可得向量的数量积为0.
的应用,即若知道向量垂直,则可得向量的数量积为0.
 ,并且
,并且  ,整理可得
,整理可得  ,将
,将  代回原式可得
代回原式可得  ,即可得到
,即可得到 ,即
,即 ,再
,再根据向量的夹角公式可求答案.
解答:解:因为
 ,
,所以
 ,
,因为
 ,
,所以
 ,
,两式相减得
 ,
,所以
 ,
,将
 代回第一个式子可得:
代回第一个式子可得: ,
,所以
 ,即
,即 .
.设向量
 与
与  的夹角为θ,则
的夹角为θ,则  =
= ,
,所以向量
 与
与  的夹角大小为
的夹角大小为 .
.故答案为:
 .
.点评:本题主要考查了平面向量的数量积的性质:若
 ?
? 的应用,即若知道向量垂直,则可得向量的数量积为0.
的应用,即若知道向量垂直,则可得向量的数量积为0. 
练习册系列答案
相关题目
设![]() ,
,![]() 是两个非零向量( )
是两个非零向量( )
|
| A. | 若| | B. | 若 |
|
| C. | 若| | D. | 若存在实数λ,使得 |
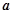 ,
,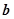 是两个非零向量( )
是两个非零向量( )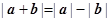 ,则
,则
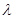 ,使得
,使得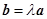
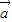 ,
,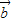 是两个非零向量,下列说法正确的是( )
是两个非零向量,下列说法正确的是( ) =
=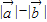 ,则
,则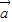 ⊥
⊥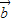
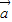 ⊥
⊥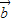 ,则
,则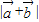 =
=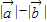
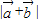 =
=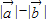 ,则存在实数λ,使得
,则存在实数λ,使得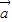 =λ
=λ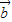
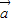 =λ
=λ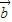 ,则
,则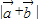 =
=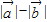
 ,
, 是两个非零向量( )
是两个非零向量( ) +
+ |=|
|=| |-|
|-| |,则
|,则 ⊥
⊥
 ⊥
⊥ ,则|
,则| +
+ |=|
|=| |-|
|-| |
| +
+ |=|
|=| |-|
|-| |,则存在实数λ,使得
|,则存在实数λ,使得 =λ
=λ
 =λ
=λ ,则|
,则| +
+ |=|
|=| |-|
|-| |
|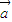 ,
,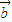 是两个非零向量,则“向量
是两个非零向量,则“向量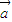 ,
,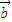 的夹角为锐角”是“函数f(x)=(x
的夹角为锐角”是“函数f(x)=(x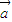 +
+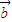 )•(
)•(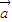 -x
-x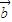 )的图象是一条开口向下的抛物线”的( )
)的图象是一条开口向下的抛物线”的( )