题目内容
试用定义证明函数f(x)=
在区间［0,1］上的单调性.
证明：任取0≤x1＜x2≤1,有0≤ 又f（x）= ∴f（x1）-f（x2）= ∴f（x1）＜f（x2），即f（x）在［0，1］上是增函数.
≤
≤1，1-
＞0，1-
＞0.
=-1+
得f（x1）=-1+
,f（x2）=-1+
.
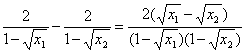＜0.
练习册系列答案
赢在中考全程优化单元滚动测试卷系列答案
赢在中考广东经济出版社系列答案
迎战新考场系列答案
语文同步解析与测评系列答案
语文同步练习册系列答案
语文同步练习系列答案
学习与实践系列答案
英语学习手册1课多练系列答案
君杰文化指导用书系列答案
英语听力训练系列答案
相关题目
有如下性质：如果常数
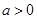，那么该函数在
上是减函数，在
上是增函数；
在
上是减函数，在
上是增函数，求
的值；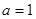
时，试用函数单调性的定义证明函数f(x)在
上是减函数。
，求函数
的最大值和最小值；
有如下性质：如果常数
，那么该函数在
上是减函数，在
上是增函数；
在
上是减函数，在
上是增函数，求
的值；
时，试用函数单调性的定义证明函数f(x)在
上是减函数。
，求函数
的最大值和最小值；
，