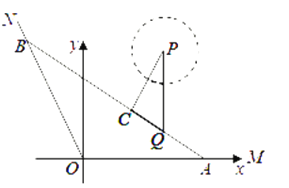
题目内容
【题目】已知数列![]() 的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.设数列
的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.设数列![]() 的前n项和为
的前n项和为![]() 且满足
且满足![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() 求正整数
求正整数![]() 的值;
的值;
(3)是否存在正整数![]() ,使得
,使得![]() 恰好为数列
恰好为数列![]() 的一项?若存在,求出所有满足条件的正整数
的一项?若存在,求出所有满足条件的正整数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
【答案】(1)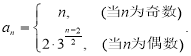 (2)
(2)![]() (3)存在两个正整数
(3)存在两个正整数![]() ;
;![]() 1或2
1或2
【解析】
(1)设![]() 的奇数项构成的等差数列的公差为
的奇数项构成的等差数列的公差为![]() ,偶数项构成的等比数列的公比为
,偶数项构成的等比数列的公比为![]() ,运用通项公式,解方程可得
,运用通项公式,解方程可得![]() ,
,![]() ,即可得到所求通项公式;(2)当
,即可得到所求通项公式;(2)当![]() 为奇数时,当
为奇数时,当![]() 为偶数时,运用通项公式,解方程可得
为偶数时,运用通项公式,解方程可得![]() 的值;(3)求得
的值;(3)求得![]() ,
,![]() ,若
,若![]() 为数列
为数列![]() 中的一项,整理化简求得
中的一项,整理化简求得![]() ,
,![]() 的值,再由数学归纳法证明,即可得到结论.
的值,再由数学归纳法证明,即可得到结论.
(1)设![]() 的奇数项构成的等差数列的公差为
的奇数项构成的等差数列的公差为![]() 偶数项构成的等比数列的公比为
偶数项构成的等比数列的公比为![]() 则
则![]()
由已知,得![]()
故数列![]() 的通项公式为:
的通项公式为: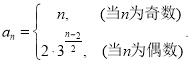
(2)当k为奇数时,由![]() 得
得![]()
由于![]() 而
而![]() 仅在
仅在![]() 时为正整数,与
时为正整数,与![]() 为奇数矛盾!
为奇数矛盾!
当k为偶数时,由![]() 得
得![]()
综上,得![]()
(3)由(1)可求得![]()
![]()
若![]() 为数列
为数列![]() 中的一项,则
中的一项,则![]() (
(![]() 为正奇数)或
为正奇数)或![]() (
(![]() 为正偶数)
为正偶数)
(i)若![]() (
(![]() 为正奇数),则
为正奇数),则![]()
当![]() 时,
时,![]() ,结论成立;
,结论成立;
当![]() 时,
时,![]() 由
由![]() 得
得![]() 解得
解得![]()
由于![]() 为正奇数,故此时满足条件的正整数k不存在.
为正奇数,故此时满足条件的正整数k不存在.
(ii)若![]() (
(![]() 为正偶数),
为正偶数),
显然![]() ,则
,则
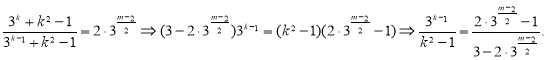
由![]() 得
得![]() 得
得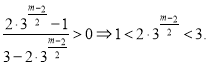
由![]() 为正偶数得
为正偶数得![]() 为正偶数,因此
为正偶数,因此![]() ,从而
,从而![]()
当![]() 时,
时,![]() ;下面用数学归纳法证明:当
;下面用数学归纳法证明:当![]() 时,
时,![]()
①当![]() 时,显然
时,显然![]() ;
;
②假设当![]() 时,有
时,有![]() ;则当
;则当![]() 时,
时,
由![]() 得
得![]() ,
,
故![]()
即![]() 时,结论成立.
时,结论成立.
由①,②知:![]() 时,
时,![]()
综合(i),(ii)得:存在两个正整数![]() ,
,![]() 1或2,使
1或2,使![]() 为数列
为数列![]() 中的项.
中的项.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目