题目内容
【题目】已知函数f(x)=x2+(x-1)|x-a|.
(1)若a=-1,解方程f(x)=1;
(2)若函数f(x)在R上单调递增,求实数a的取值范围;
(3)是否存在实数a,使不等式f(x)≥2x-3对任意x∈R恒成立?若存在,求出a的取值范围;若不存在,请说明理由.
【答案】(1){x|x≤-1或x=1};(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)把![]() 代入函数解析式,分段后分段求解方程
代入函数解析式,分段后分段求解方程![]() 的解集,取并集后得答案;(2)分段写出函数
的解集,取并集后得答案;(2)分段写出函数![]() 的解析式,由
的解析式,由![]() 在
在![]() 上单调递增,则需第一段二次函数的对称轴小于等于
上单调递增,则需第一段二次函数的对称轴小于等于![]() ,第二段一次函数的一次项系数大于0,且第二段函数的最大值小于等于第一段函数的最小值,联立不等式组后求解
,第二段一次函数的一次项系数大于0,且第二段函数的最大值小于等于第一段函数的最小值,联立不等式组后求解![]() 的取值范围;(3)把不等式
的取值范围;(3)把不等式![]() 对一切实数
对一切实数![]() 恒成立转化为函数
恒成立转化为函数![]() 对一切实数
对一切实数![]() 恒成立,然后对
恒成立,然后对![]() 进行分类讨论,利用函数单调性求得
进行分类讨论,利用函数单调性求得![]() 的范围,取并集后得答案.
的范围,取并集后得答案.
试题解析:(1)当![]() 时,
时, ![]() ,则
,则![]() ;当
;当![]() 时,由
时,由![]() ,得
,得![]() ,解得
,解得![]() 或
或![]() ;当
;当![]() 时,
时, ![]() 恒成立,∴方程的解集为
恒成立,∴方程的解集为![]() 或
或![]() .
.
(2)由题意知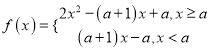 ,若
,若![]() 在R上单调递增,则
在R上单调递增,则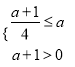 解得
解得![]() ,∴实数
,∴实数![]() 的取值范围为
的取值范围为![]() .
.
(3)设![]() ,则
,则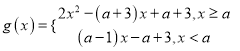 ,不等式
,不等式![]() 对任意
对任意![]() 恒成立,等价于不等式
恒成立,等价于不等式![]() 对任意
对任意![]() 恒成立.
恒成立.
①若![]() ,则
,则![]() ,即
,即![]() ,取
,取![]() ,此时
,此时![]() ,∴
,∴![]() ,即对任意的
,即对任意的![]() ,总能找到
,总能找到![]() ,使得
,使得![]() ,∴不存在
,∴不存在![]() ,使得
,使得![]() 恒成立.
恒成立.
②若![]() ,则
,则![]() ,∴
,∴![]() 的值域为
的值域为![]() ,∴
,∴![]() 恒成立③若
恒成立③若![]() ,当
,当![]() 时,
时, ![]() 单调递减,其值域为
单调递减,其值域为![]() ,由于
,由于![]() ,所以
,所以![]() 恒成立,当
恒成立,当![]() 时,由
时,由![]() ,知
,知![]() ,
, ![]() 在
在![]() 处取得最小值,令
处取得最小值,令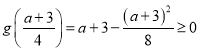 ,得
,得![]() ,又
,又![]() ,∴
,∴![]() ,综上,
,综上, ![]() .
.

练习册系列答案
相关题目