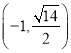题目内容
【题目】已知函数![]() ,若
,若![]() 在
在![]() 处的切线为
处的切线为![]() .
.
(Ⅰ)求实数![]() ,
,![]() 的值;
的值;
(Ⅱ)若不等式![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(Ⅲ)设![]() 其中
其中![]() ,证明:
,证明:
![]()
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)证明见解析
;(Ⅲ)证明见解析
【解析】
(Ⅰ)求出![]() ,
,![]() ,建立
,建立![]() 方程,求解即可得到结论;
方程,求解即可得到结论;
(Ⅱ)结合(Ⅰ)中的结论,将问题转化为![]() 对任意
对任意![]() 恒成立,令
恒成立,令
![]() ,而
,而![]() 是偶函数,只需
是偶函数,只需![]() 时,
时,![]() 恒成立,注意
恒成立,注意![]() ,只需
,只需![]() 在
在![]() 单调递增即可,若存在
单调递增即可,若存在![]() 单调递减,则
单调递减,则![]() 不恒成立,转化为研究
不恒成立,转化为研究![]() 在
在![]() 单调性,即可求解;
单调性,即可求解;
(Ⅲ)由![]() ,利用(Ⅱ)的结论,可得
,利用(Ⅱ)的结论,可得![]() ,
,![]() .进而得到
.进而得到
![]() ,将
,将![]() 分别用
分别用![]() ,
,![]() 代入得到
代入得到![]() 个不等式,相加即可证明结论.
个不等式,相加即可证明结论.
(Ⅰ)由![]() ,得
,得![]() ;
;
由![]() ,得
,得![]() .
.
根据题意可得![]() ,解得
,解得![]() ;
;
(Ⅱ)解法一:由不等式![]() 对任意
对任意![]() 恒成立知
恒成立知![]() 恒成立,令
恒成立,令![]() ,
,
显然![]() 为偶函数,故当
为偶函数,故当![]() 时,
时,![]() 恒成立.
恒成立.
![]() ,令
,令![]() ,
,
![]() ,令
,令![]() ,
,
显然![]() 为
为![]() 上的增函数,故
上的增函数,故![]() ,
,
即![]() 在
在![]() 上单调递增,
上单调递增,![]() .
.
①当![]() ,即
,即![]() 时,
时,![]() ,
,
则有![]() 在
在![]() 上单调递增,故
上单调递增,故![]() ,
,
则![]() 在
在![]() 上单调递增,故
上单调递增,故![]() ,符合题意;
,符合题意;
②当![]() ,即
,即![]() 时,因为
时,因为![]() ,
,
故存在![]() ,使得
,使得![]() ,
,
故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() ,
,
故![]() 在
在![]() 上单谓递减,故
上单谓递减,故![]() 与
与![]() 矛盾.
矛盾.
综上,![]() .
.
解法二:由不等式![]() 对任意
对任意![]() 恒成立,
恒成立,
知![]() 恒成立,当
恒成立,当![]() 时,不等式成立;
时,不等式成立;
当![]() 时,
时,![]() ,令
,令![]() ,
,
由于![]() 为偶函数,故只需考虑
为偶函数,故只需考虑![]() 的情况即可.
的情况即可.
当![]() 时,
时,![]() .
.
令![]() ,
,![]() ,
,
令![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上单调递增,
上单调递增,
故![]() .
.
因此当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上单调递增,
上单调递增,
即有![]() ,故
,故![]() ,
,
所以![]() 在
在![]() 上单调递增,由洛必达法则有
上单调递增,由洛必达法则有![]() ,故
,故![]() .
.
(Ⅲ)解法一:
![]() ,
,
由(Ⅱ)![]() ,当且仅当
,当且仅当![]() 时,等号成立;
时,等号成立;![]() ,当且仅当
,当且仅当![]() 时,等号成立.故
时,等号成立.故![]() ,当且仅当
,当且仅当![]() 时等号成立.
时等号成立.
因此有![]() ,
,
![]() ,
,
![]()
以上![]() 个式子相加得
个式子相加得
![]()
![]() .
.
解法二:由(Ⅱ)知![]() ,
,
当且仅当![]() 时等号同时成立.
时等号同时成立.
故![]() ,
,
![]() ,
,
![]()
以上![]() 个式子相加得
个式子相加得
![]()
![]() .
.

【题目】某商场经销某商品,根据以往资料统计,顾客采用的付款期数![]() 的分布列为
的分布列为
| 1 | 2 | 3 | 4 | 5 |
P | 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为250元;分4期或5期付款,其利润为300元,X表示经销一件该商品的利润.
(1)求事件A:“购买该商品的3位顾客中,至少有1位采用1期付款”的概率![]() ;
;
(2)求X的分布列及期望![]() .
.