题目内容
已知A,B,C为锐角△ABC的三个内角,向量 =(2-2sinA,cosA+sinA)与
=(2-2sinA,cosA+sinA)与 =(sinA-cosA,1+sinA)共线.
=(sinA-cosA,1+sinA)共线.
(1)求角A的大小;
(2)求函数 的值域.
的值域.
解:(1) =(sinA-cosA,1+sinA)且
=(sinA-cosA,1+sinA)且 共线,得
共线,得
(2-2sinA)(1+sinA)-(sinA-cosA)(cosA+sinA)=0
化简,得sinA=±
又△ABC是锐角三角形∴sinA=
(2)由A= 得B+C=
得B+C= ,即C=
,即C= -B
-B
y=2sin2B+cos
=1-cos2B+cos sin2B
sin2B
=1+sin2Bcos
∵
∴ <2B<π∴
<2B<π∴
∴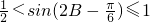 .故
.故
因此函数y=2sin2B+cos 的值域为(
的值域为( ,2]
,2]
分析:(1)由已知 ,利用向量共线的条件及A为锐角整理可得,sinA=
,利用向量共线的条件及A为锐角整理可得,sinA= ,从而可求
,从而可求
(2)结合(1)中的条件可把所求函数式化简得, ,利用辅助角公式可得
,利用辅助角公式可得
y=sin2B- )+1,结合题中锐角三角形的条件可求B的范围,进而求出函数的值域
)+1,结合题中锐角三角形的条件可求B的范围,进而求出函数的值域
点评:本题主要考查了向量平行的坐标表示,特殊角的三角函数值,和差角公式的运用,正弦函数的值域的求解等知识,综合的知识较多,但都是基本方法的考查,要求考生具备扎实的基本功.熟练的运用知识
 =(sinA-cosA,1+sinA)且
=(sinA-cosA,1+sinA)且 共线,得
共线,得(2-2sinA)(1+sinA)-(sinA-cosA)(cosA+sinA)=0
化简,得sinA=±

又△ABC是锐角三角形∴sinA=

(2)由A=
 得B+C=
得B+C= ,即C=
,即C= -B
-By=2sin2B+cos

=1-cos2B+cos
 sin2B
sin2B=1+sin2Bcos

∵

∴
 <2B<π∴
<2B<π∴
∴
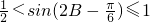 .故
.故
因此函数y=2sin2B+cos
 的值域为(
的值域为( ,2]
,2]分析:(1)由已知
 ,利用向量共线的条件及A为锐角整理可得,sinA=
,利用向量共线的条件及A为锐角整理可得,sinA= ,从而可求
,从而可求(2)结合(1)中的条件可把所求函数式化简得,
 ,利用辅助角公式可得
,利用辅助角公式可得y=sin2B-
 )+1,结合题中锐角三角形的条件可求B的范围,进而求出函数的值域
)+1,结合题中锐角三角形的条件可求B的范围,进而求出函数的值域点评:本题主要考查了向量平行的坐标表示,特殊角的三角函数值,和差角公式的运用,正弦函数的值域的求解等知识,综合的知识较多,但都是基本方法的考查,要求考生具备扎实的基本功.熟练的运用知识

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 =(2-2sinA,cosA+sinA),
=(2-2sinA,cosA+sinA), =(1+sinA,cosA-sinA),且
=(1+sinA,cosA-sinA),且 ⊥
⊥ .
. -2B)取最大值时角B的大小.
-2B)取最大值时角B的大小. =(2-2sinA,cosA+sinA),
=(2-2sinA,cosA+sinA), =(1+sinA,cosA-sinA),且
=(1+sinA,cosA-sinA),且 ⊥
⊥ .
. -2B)取最大值时角B的大小.
-2B)取最大值时角B的大小.