题目内容
已知向量 ,
,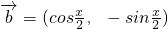 ,且
,且
(1)求 并判断x为何值时
并判断x为何值时 ;
;
(2)若 的最小值是
的最小值是 ,求λ的值.
,求λ的值.
解:(1)∵ =( cos
=( cos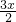 +cos
+cos ,sin
,sin 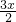 -sin
-sin ),故
),故  2=2+2cos2x=4cos2x.
2=2+2cos2x=4cos2x.
因为 ,所以
,所以 =2cosx. 再由
=2cosx. 再由  ,
,
若 ,则
,则 ,所以
,所以 时,
时, .
.
(2)∵ =2(cosx-λ)2-1-2λ2,
=2(cosx-λ)2-1-2λ2,
因为 ,所以cosx∈[0,1].
,所以cosx∈[0,1].
讨论:若λ<0时,f(x)min=-1,矛盾.
若0≤λ≤1时, =-
=- ,解得
,解得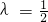 .
.
若λ>1时,f(x)min=1-4λ=- ,解得
,解得 ,矛盾.
,矛盾.
综合可得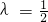 .
.
分析:(1)先求出 的坐标,从而求出
的坐标,从而求出 的值,从而求得
的值,从而求得 =2cosx.再由
=2cosx.再由  ,求出
,求出 时x的值.
时x的值.
(2)化简函数f(x)的解析式为2(cosx-λ)2-1-2λ2,分λ<0、0≤λ≤1、λ>1三种情况,根据函数的最小值等于 分必然求出λ的值.
分必然求出λ的值.
点评:本题主要考查两个向量数量积公式的应用,余弦函数的定义域和值域,求二次函数在闭区间上的最值,体现了分类讨论的数学思想,属于中档题.
 =( cos
=( cos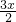 +cos
+cos ,sin
,sin 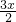 -sin
-sin ),故
),故  2=2+2cos2x=4cos2x.
2=2+2cos2x=4cos2x.因为
 ,所以
,所以 =2cosx. 再由
=2cosx. 再由  ,
,若
 ,则
,则 ,所以
,所以 时,
时, .
.(2)∵
 =2(cosx-λ)2-1-2λ2,
=2(cosx-λ)2-1-2λ2,因为
 ,所以cosx∈[0,1].
,所以cosx∈[0,1].讨论:若λ<0时,f(x)min=-1,矛盾.
若0≤λ≤1时,
 =-
=- ,解得
,解得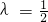 .
.若λ>1时,f(x)min=1-4λ=-
 ,解得
,解得 ,矛盾.
,矛盾.综合可得
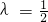 .
.分析:(1)先求出
 的坐标,从而求出
的坐标,从而求出 的值,从而求得
的值,从而求得 =2cosx.再由
=2cosx.再由  ,求出
,求出 时x的值.
时x的值.(2)化简函数f(x)的解析式为2(cosx-λ)2-1-2λ2,分λ<0、0≤λ≤1、λ>1三种情况,根据函数的最小值等于
 分必然求出λ的值.
分必然求出λ的值.点评:本题主要考查两个向量数量积公式的应用,余弦函数的定义域和值域,求二次函数在闭区间上的最值,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
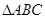 中,
中, 、
、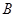 、
、 所对的边分别为
所对的边分别为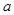 、
、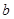 、
、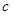 .已知向量
.已知向量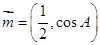 ,
, ,且
,且 .
.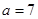 ,
,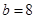 ,求
,求 ,
,
 ,且
,且 ∥
∥ ,
, ,且△ABC的面积小于
,且△ABC的面积小于 ,求角B的取值范围.
,求角B的取值范围.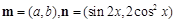 ,若
,若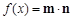 且
且
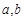 的值;
的值;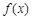 的最大值及取得最大值时的
的最大值及取得最大值时的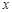 的集合;
的集合; ,
, ,且
,且
 的取值范围;
的取值范围; 的最小值,并求此时x的值
的最小值,并求此时x的值 ,
, ,且
,且 .
. 及
及 ;
; 的最大值,并求使函数取得最大值时
的最大值,并求使函数取得最大值时 的
的