题目内容
14. 如图,正三棱锥O-ABC的三条侧棱OA,OB,OC两两垂直,且OA=OB=OC=2.E、F分别是AB、AC的中点,过EF作平面与侧棱OA,OB,OC或其延长线分别相交于A1、B1、C1.
如图,正三棱锥O-ABC的三条侧棱OA,OB,OC两两垂直,且OA=OB=OC=2.E、F分别是AB、AC的中点,过EF作平面与侧棱OA,OB,OC或其延长线分别相交于A1、B1、C1.(Ⅰ)求证:直线B1C1∥平面ABC;
(Ⅱ)若OA1=$\frac{3}{2}$,求二面角O-A1B1-C1的余弦值.
分析 (Ⅰ)证明EF∥面OBC,可得EF∥B1C1,即可证明:直线B1C1∥平面ABC;
(Ⅱ)若OA1=$\frac{3}{2}$,以OA,OB,OC为X轴,Y轴,Z轴建立空间直角坐标系,求出平面的法向量,利用向量的夹角公式求二面角O-A1B1-C1的余弦值.
解答 (Ⅰ)证明:∵E,F分别是AB,AC的中点,∴EF∥BC
又∵EF?面OBC,∴EF∥面OBC …(2分)
∵面A1B1C1∩面OBC=B1C1,EF?面A1B1C1∩
∴EF∥B1C1…(4分)
又∵B1C1?面ABC,∴B1C1∥面ABC …(6分)
(Ⅱ)解:如图,以OA,OB,OC为X轴,Y轴,Z轴建立空间直角坐标系,则O(0,0,0),
A(2,0,0),B(0,2,0),C(0,0,2),E(1,1,0),F(1,0,1),…(8分)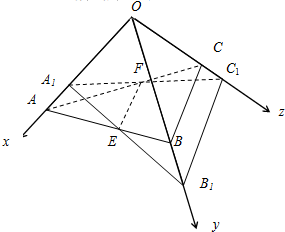
∵B1∈OB,设B1(0,m,0),又∵点B1∈平面A1EF,
∴$\overrightarrow{O{B_1}}=λ\overrightarrow{OE}+μ\overrightarrow{OF}+(1-λ-μ)\overrightarrow{O{A_1}}=(\frac{-(λ+μ)+3}{2},λ,μ)=(0,m,0)$,
解得m=3
∴B1(0,3,0),同理C1(0,0,3)…(10分)
设平面A1B1C1的法向量为m=(x,y,z),$\overrightarrow{{A_1}{B_1}}=(-\frac{3}{2},3,0),\overrightarrow{{A_1}{C_1}}=(-\frac{3}{2},0,3)$,$m•\overrightarrow{{A_1}{B_1}}=-\frac{3}{2}x+3y=0$,$m•\overrightarrow{{A_1}{C_1}}=-\frac{3}{2}x+3z=0$,取m=(2,1,1),…(12分)
又知平面OA1B1即平面OAB的法向量为n=(0,0,1),设二面角O-A1B1-C1为θ,
∵二面角O-A1B1-C1为锐角,∴$cosθ=|\frac{m•n}{|m|•|n|}|=\frac{1}{{1•\sqrt{6}}}=\frac{{\sqrt{6}}}{6}$,…(14分)
∴二面角O-A1B1-C1的余弦值为$\frac{{\sqrt{6}}}{6}$. …(15分)
点评 本题考查线面平行的判定与性质,考查二面角的余弦值,考查向量方法的运用,属于中档题.

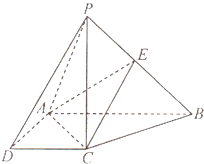 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,AB∥DC,∠ADC=90°,PC=AB=2AD=2DC=2,点E为PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,AB∥DC,∠ADC=90°,PC=AB=2AD=2DC=2,点E为PB的中点. (
(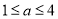 且
且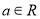 )个单位的洗衣粉液在一定量水的洗衣机中,它在水中释放的浓度
)个单位的洗衣粉液在一定量水的洗衣机中,它在水中释放的浓度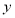 (克/升)随着时间
(克/升)随着时间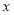 (分钟)变化的函数关系式近似为
(分钟)变化的函数关系式近似为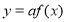 ,其中
,其中 ,若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和,根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起有效去污的作用.
,若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和,根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起有效去污的作用.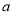 个单位的洗衣液,要使接下来的4分钟中能够持续有效去污,试求
个单位的洗衣液,要使接下来的4分钟中能够持续有效去污,试求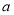 的最小值(精确到0.1,参考数据:
的最小值(精确到0.1,参考数据: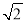 取
取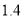 ).
).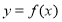 经过点
经过点 ,则
,则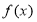 是( )
是( ) 上是增函数
上是增函数