题目内容
已知:向量 =(sin
=(sin ,1-cosθ),
,1-cosθ), =(cos
=(cos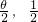 ),(O为坐标原点).
),(O为坐标原点).
(1)求 的最大值及此时θ的值组成的集合;
的最大值及此时θ的值组成的集合;
(2)若A点在直线y=2x+m上运动,求实数m的取值范围.
解:(1) =
= ,(4分)
,(4分)
 (k∈Z)时,
(k∈Z)时, .(9分)
.(9分)
(2)将A点坐标代入直线方程得:
 =
=
∵
∴ (14分)
(14分)
分析:(1)利用向量的数量积公式求出两个向量的数量积,令 ,求出最大值.
,求出最大值.
(2)将A的坐标代入直线的方程表示出m,利用三角函数的二倍角公式化简m的解析式;再对m的解析式配方,求出m的范围.
点评:本题考查向量的数量积公式、考查三角函数的和差角公式、二倍角公式、求三角函数最值的方法:整体角处理.
 =
= ,(4分)
,(4分) (k∈Z)时,
(k∈Z)时, .(9分)
.(9分)(2)将A点坐标代入直线方程得:
 =
=
∵

∴
 (14分)
(14分)分析:(1)利用向量的数量积公式求出两个向量的数量积,令
 ,求出最大值.
,求出最大值.(2)将A的坐标代入直线的方程表示出m,利用三角函数的二倍角公式化简m的解析式;再对m的解析式配方,求出m的范围.
点评:本题考查向量的数量积公式、考查三角函数的和差角公式、二倍角公式、求三角函数最值的方法:整体角处理.

练习册系列答案
相关题目
已知:向量
=(sin
,1-cosθ),
=(cos
,
),(O为坐标原点).
(1)求
•
的最大值及此时θ的值组成的集合;
(2)若A点在直线y=2x+m上运动,求实数m的取值范围.
| OA |
| θ |
| 2 |
| OB |
| θ |
| 2 |
| 1 |
| 2 |
(1)求
| OA |
| OB |
(2)若A点在直线y=2x+m上运动,求实数m的取值范围.
已知平面向量
=(sinθ,1),
=(-
,cosθ),若
⊥
,则θ可以为( )
| a |
| b |
| 3 |
| a |
| b |
A、θ=
| ||
B、θ=
| ||
C、θ=
| ||
D、θ=
|
 =(sinθ,1),
=(sinθ,1), =(-
=(- ,cosθ),若
,cosθ),若 B.θ=
B.θ=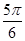 C.θ=
C.θ= D.θ=
D.θ=