题目内容

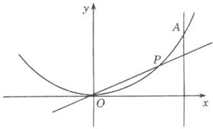
设点P在曲线y=x2上，从原点向A（2，4）移动，如果直线OP，曲线y=x2及直线x=2所围成的面积分别记为S1、S2．
（Ⅰ）当S1=S2时，求点P的坐标；
（Ⅱ）当S1+S2有最小值时，求点P的坐标和最小值．
（Ⅰ）设点P的横坐标为t（0＜t＜2），则P点的坐标为（t，t2），
直线OP的方程为y=tx
S1=∫0t（tx-x2）dx=
1
6
t3，S2=∫t2（x2-tx）dx=
8
3
-2t+
1
6
t3，
因为S1=S2，，所以t=
4
3
，点P的坐标为（
4
3
，
16
9
）
S=S1+S2=
1
6
t3+
8
3
-2t+
1
6
t3=
1
3
t3-2t+
8
3

S′=t2-2，令S'=0得t2-2=0，t=
2

因为0＜t＜
2
时，S'＜0；
2
＜t＜2时，S'＞0
所以，当t=
2
时，Smin=
8-4
2
3
，P点的坐标为（
2
，2）．
练习册系列答案
相关题目
如图，直线y=kx+b与椭圆
x2
4
+y2=1交于A，B两点，记△AOB的面积为S．
（I）求在k=0，0＜b＜1的条件下，S的最大值；
（Ⅱ）当|AB|=2，S=1时，求直线AB的方程．
已知斜率为1的直线l过椭圆
x2
4
+y2=1的右焦点F2．
（1）求直线l的方程；
（2）若l与椭圆交于点A、B两点，F1为椭圆左焦点，求S△F1AB．
如图，已知椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)过点(1，
2
2
)，离心率为
2
2
，左、右焦点分别为F1、F2．点P为直线l：x+y=2上且不在x轴上的任意一点，直线PF1和PF2与椭圆的交点分别为A、B和C、D，O为坐标原点．设直线PF1、PF2的斜率分别为k1、k2．
（Ⅰ）证明：
1
k1
-
3
k2
=2；
（Ⅱ）问直线l上是否存在点P，使得直线OA、OB、OC、OD的斜率kOA、kOB、kOC、kOD满足kOA+kOB+kOC+kOD=0？若存在，求出所有满足条件的点P的坐标；若不存在，说明理由．
已知椭圆C的中心在原点，焦点在x轴上．若椭圆上的点A(1，
3
2
)到焦点F1、F2的距离之和等于4．
（1）写出椭圆C的方程和焦点坐标．
（2）过点Q（1，0）的直线与椭圆交于两点M、N，当△OMN的面积取得最大值时，求直线MN的方程．
如图，已知圆C1的方程为(x-2)2+(y-1)2=
20
3
，椭圆C2的方程为
x2
a2
+
y2
b2
=1（a＞b＞0），C2的离心率为
2
2
，如果C1与C2相交于A、B两点，且线段AB恰为圆C1的直径，求直线AB的方程和椭圆C2的方程．
抛物线y2=4x的一条弦被点A（4，2）平分，那么这条弦所在的直线方程式为______．
过x轴上动点A（a，0）引抛物线y=x2+1的两条切线AP、AQ，P、Q为切点．
（1）若切线AP，AQ的斜率分别为k1和k2，求证：k1•k2为定值，并求出定值；
（2）求证：直线PQ恒过定点，并求出定点坐标；
（3）当
S△APO
PQ
最小时，求
AQ
•
AP
的值．
在平面直角坐标系xOy中，△ABC的顶点B、C的坐标为B（-2，0），C（2，0），直线AB，AC的斜率乘积为-
1
4
，设顶点A的轨迹为曲线E．
（1）求曲线E的方程；
（2）设曲线E与y轴负半轴的交点为D，过点D作两条互相垂直的直线l1，l2，这两条直线与曲线E的另一个交点分别为M，N．设l1的斜率为k（k≠0），△DMN的面积为S，试求
S
|k|
的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网