题目内容
AB垂直于△BCD所在的平面,AC=
,AD=
,BC:BD=3:4,当△BCD的面积最大时,点A到直线CD的距离为
.
| 10 |
| 17 |
| 13 |
| 5 |
| 13 |
| 5 |
分析:利用线面垂直的性质可得AB⊥BC,AB⊥BD,利用勾股定理可得BC、BD、AB.当∠CBD=90°时,△BCD的面积最大,CD=
.过点B作BE⊥CD,垂足为E,连接AE,则CD⊥AE.利用等面积可得BE,再利用勾股定理可得AE.
| BC2+BD2 |
解答:解:如图所示.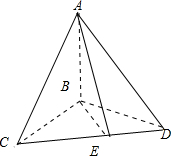 设BC=3x,则BD=4x.∵AB⊥平面BCD.
设BC=3x,则BD=4x.∵AB⊥平面BCD.
∴AB⊥BC,AB⊥BD.
在Rt△ABC中,由勾股定理可得AB=
=
.
在Rt△ABD中,同理,AB=
,
∴
=
,解得x=1.
∴BC=3,BD=4,AB=1.
当∠CBD=90°时,△BCD的面积最大,CD=
=5.
过点B作BE⊥CD,垂足为E,连接AE,则CD⊥AE.
在Rt△BCD中,BE=
=
.
∵AB⊥平面BCD,∴AB⊥BE.
∴AE=
=
=
.
故答案为
.
 设BC=3x,则BD=4x.∵AB⊥平面BCD.
设BC=3x,则BD=4x.∵AB⊥平面BCD.∴AB⊥BC,AB⊥BD.
在Rt△ABC中,由勾股定理可得AB=
| AC2-BC2 |
| 10-9x2 |
在Rt△ABD中,同理,AB=
| 17-16x2 |
∴
| 10-9x2 |
| 17-16x2 |
∴BC=3,BD=4,AB=1.
当∠CBD=90°时,△BCD的面积最大,CD=
| BC2+BD2 |
过点B作BE⊥CD,垂足为E,连接AE,则CD⊥AE.
在Rt△BCD中,BE=
| BC•BD |
| CD |
| 12 |
| 5 |
∵AB⊥平面BCD,∴AB⊥BE.
∴AE=
| AB2+BE2 |
1+(
|
| 13 |
| 5 |
故答案为
| 13 |
| 5 |
点评:本题综合考查了线面垂直的性质、勾股定理等基础知识与基本方法,属于基础题.

练习册系列答案
相关题目
 选做题(考生只能从A,B,C中选做一题,多做以所做第一题记分)
选做题(考生只能从A,B,C中选做一题,多做以所做第一题记分)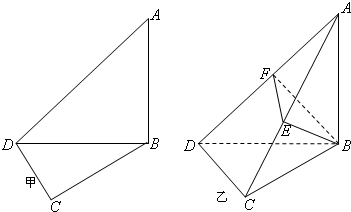
 选做题(考生只能从A,B,C中选做一题,多做以所做第一题记分)
选做题(考生只能从A,B,C中选做一题,多做以所做第一题记分)
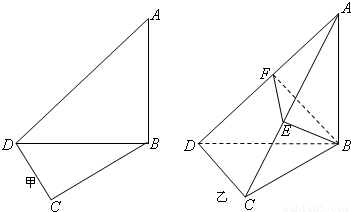
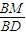 的值;若不存在,说明理由.
的值;若不存在,说明理由.