题目内容
下表是某单位在2013年1—5月份用水量(单位:百吨)的一组数据:
|
月份 |
1 |
2 |
3 |
4 |
5 |
|
用水量 |
4 5 |
4 |
3 |
2 5 |
1 8 |
(Ⅰ)若由线性回归方程得到的预测数据与实际检验数据的误差不超过0 05,视为“预测可靠”,通过公式得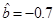 ,那么由该单位前4个月的数据中所得到的线性回归方程预测5月份的用水量是否可靠?说明理由;
,那么由该单位前4个月的数据中所得到的线性回归方程预测5月份的用水量是否可靠?说明理由;
(Ⅱ)从这5个月中任取2个月的用水量,求所取2个月的用水量之和小于7(单位:百吨)的概率
参考公式:回归直线方程是: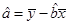 ,
,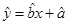
①“预测可靠” ②
【解析】
试题分析:(Ⅰ)首先计算 由于已知
由于已知 则
通过
则
通过 计算出
计算出 ,从而求出回归方程,再比较回归方程的值与实际值的差的绝对值即可 (Ⅱ)列举法:把所有可能与符合条件的一一列举即可求概率
,从而求出回归方程,再比较回归方程的值与实际值的差的绝对值即可 (Ⅱ)列举法:把所有可能与符合条件的一一列举即可求概率
试题解析:(Ⅰ)由数据,得 ,且
,且
 ,
所以
,
所以 关于
关于 的线性回归方程为
的线性回归方程为
当 时,得估计值
时,得估计值 ,
而
,
而 ;
;
所以,所得到的回归方程是“预测可靠”的 6分
(Ⅱ)从这5个月中任取2个月,包含的基本事件有以下10个:




其中所取2个月的用水量之和小于7(百吨)的基本事件有以下6个:




故所求概率 12分
12分
考点:1 统计;2 回归直线方程;3 回归分析;4 列举法求概率

城市交通拥堵已经成为日益突出的社会问题,为了缓解交通高峰的压力,某市政府采取了错时上下班的措施.下表是某路段在采取措施前后30 min通过的车流量.
|
时间段 |
6∶30~7∶00 |
7∶00~7∶30 |
7∶30~8∶00 |
|
采取措施前车流量 |
2000 |
2500 |
3000 |
|
采取措施后车流量 |
1800 |
2200 |
2500 |
|
时间段 |
8∶00~8∶30 |
8∶30~9∶00 |
9∶00~9∶30 |
|
采取措施前车流量 |
1800 |
1700 |
1600 |
|
采取措施后车流量 |
2300 |
2000 |
1800 |
在6∶30到9∶30这个时间段内,采取措施后下列说法正确的是( )
A.采取措施后平均车流量减少
B.采取措施后平均车流量增大
C.采取措施后车流量的方差大于采取措施前的
D.采取措施后车流量的方差小于采取措施前的
城市交通拥堵已经成为日益突出的社会问题,为了缓解交通高峰的压力,某市政府采取了错时上下班的措施.下表是某路段在采取措施前后30 min通过的车流量.
| 时间段 | 6∶30~7∶00 | 7∶00~7∶30 | 7∶30~8∶00 |
| 采取措施前车流量 | 2000 | 2500 | 3000 |
| 采取措施后车流量 | 1800 | 2200 | 2500 |
| 时间段 | 8∶00~8∶30 | 8∶30~9∶00 | 9∶00~9∶30 |
| 采取措施前车流量 | 1800 | 1700 | 1600 |
| 采取措施后车流量 | 2300 | 2000 | 1800 |
- A.采取措施后平均车流量减少
- B.采取措施后平均车流量增大
- C.采取措施后车流量的方差大于采取措施前的
- D.采取措施后车流量的方差小于采取措施前的