Question

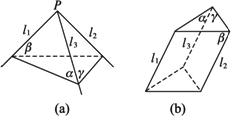
（12分）如图所示，三个平面两两相交，有三条交线，求证这三条交线交于一点或互相平行．

 

Answer 1

【答案】

见解析

【解析】

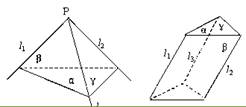
试题分析：如答图所示，设已知平面α、β、γ，α∩β＝l₁，β∩γ＝l₂，α∩γ＝l₃，如果l₁、 l₂、 l₃中有任意两条交于一点P，设l₁∩ l₂＝P，即P∈l₁，P∈l₂，那么P∈α，P∈γ，则点P在平面α、γ的交线l3上，即l₁、 l₂、 l₃交于一点如（a）图；如果l₁、 l₂、 l₃中任何两条都不相交，那么，因为任意两条都共面，所以l₁∥ l₂∥ l₃如（b）图.

考点：本题主要考查点线面关系的平行关系。

点评：平行关系中，平行的定义及平行关系的性质，往往要综合在一起运用。