题目内容
6．${（3\sqrt{5}）^2}•{（-\frac{8}{27}）^{\frac{2}{3}}}+{（0.002）^{-\frac{1}{2}}}-10{（\sqrt{5}-2）^{-1}}+{（\sqrt{3}-\sqrt{2}）^0}$=（ ）| A． | $-39-20\sqrt{5}$ | B． | 0 | C． | 1 | D． | -39 |
分析 化简${（3\sqrt{5}）^2}•{（-\frac{8}{27}）^{\frac{2}{3}}}+{（0.002）^{-\frac{1}{2}}}-10{（\sqrt{5}-2）^{-1}}+{（\sqrt{3}-\sqrt{2}）^0}$=32•5•$（\frac{2}{3}）^{3×\frac{2}{3}}$+$\sqrt{500}$-10（$\sqrt{5}$+2）+1，从而求得．
解答 解：${（3\sqrt{5}）^2}•{（-\frac{8}{27}）^{\frac{2}{3}}}+{（0.002）^{-\frac{1}{2}}}-10{（\sqrt{5}-2）^{-1}}+{（\sqrt{3}-\sqrt{2}）^0}$
=32•5•$（\frac{2}{3}）^{3×\frac{2}{3}}$+$\sqrt{500}$-10（$\sqrt{5}$+2）+1
=20+10$\sqrt{5}$-10$\sqrt{5}$-20+1=1；
故选：C．
点评 本题考查了有理数指数幂的化简与求值．
练习册系列答案
相关题目
17．已知点$P（{sin\frac{2π}{3}，cos\frac{2π}{3}}）$落在角θ的终边上，则tanθ=（ ）
| A． | -$\sqrt{3}$ | B． | $\frac{{\sqrt{3}}}{3}$ | C． | -$\frac{{\sqrt{3}}}{3}$ | D． | $\sqrt{3}$ |
14．等差数列{an}{bn}前n项和分别为An和Bn，$\frac{A_n}{B_n}=\frac{7n+1}{4n+27}$，则$\frac{{{a_3}+{a_{19}}}}{{{b_8}+{b_{14}}}}$等于（ ）
| A． | $\frac{7}{4}$ | B． | $\frac{4}{3}$ | C． | $\frac{3}{2}$ | D． | $\frac{78}{71}$ |
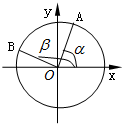如图，在平面直角坐标系xoy中，以ox轴为始边作一个锐角α和一个钝角β，它们的终边分别与单位圆相交于点A和点B．且点A的坐标为$（\frac{{\sqrt{5}}}{5}，\frac{{2\sqrt{5}}}{5}）$，点B的坐标为$（-\frac{{3\sqrt{10}}}{10}，\frac{{\sqrt{10}}}{10}）$．
15．函数f（x）=$\frac{ax+1}{x+2}$在区间（-2，+∞）上单调递增，则a的取值范围是（ ）
| A． | $（{0，\frac{1}{2}}）$ | B． | （-∞，-1）∪（1，+∞） | C． | $（{\frac{1}{2}，+∞}）$ | D． | （-2，+∞） |
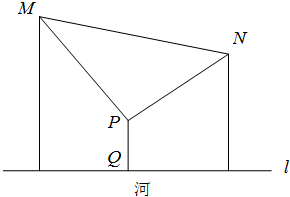如图，相距14km的两个居民小区M和N位于河岸l（直线）的同侧，M和N距离河岸分别为10km和8km．现要在河的小区一侧选一地点P，在P处建一个生活污水处理站，从P排直线水管PM，PN分别到两个小区和垂直于河岸的水管PQ，使小区污水经处理后排入河道．设PQ段长为t km（0＜t＜8）．