题目内容
下表是降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨)标准煤的几组对应数据,根据表中提供的数据,求出y关于x的线性回归方程  ,那么表中m的值为( )
,那么表中m的值为( )
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | m | 4 | 4.5 |
D
解析试题分析:由已知, =4.5,代入
=4.5,代入 得
得 。由
。由 =3.5,得,m=,3,故选D。
=3.5,得,m=,3,故选D。
考点:本题主要考查线性回归直线方程。
点评:简单题,线性回归直线过样本中心点( )。
)。

练习册系列答案
相关题目
在样本的频率分布直方图中, 共有9个小长方形, 若第一个长方形的面积为0.02, 前五个与后五个长方形的面积分别成等差数列且公差互为相反数,若样本容量为160, 则中间一组(即第五组)的频数为( )
| A.12 | B.24 | C.36 | D.48 |
一个容量为35的样本数据,分组后,组距与频数如下: 个;
个; 个;
个; 个;
个; 个;
个; 个;
个;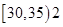 个。则样本在区间
个。则样本在区间 上的频率为
上的频率为
| A.20% | B.69% | C.31% | D.27% |
随机抽取某中学甲、乙两面个班10名同学,测量他们的身高(单位:cm)后获得身高数据的茎叶图如图甲所示,在这20人中,记身高在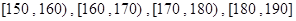 内的人数依次为
内的人数依次为 ,图乙是统计样本中身高在一定范围内的人数的算法流程图,则下列说法正确的是( )
,图乙是统计样本中身高在一定范围内的人数的算法流程图,则下列说法正确的是( )



| A.由图甲可知甲、乙两班中身高的中位数较大的是甲班,图乙输出的S的值为18 |
| B.由图甲可知甲、乙两班中身高的中位数较大的是乙班,图乙输出的S的值为18 |
| C.由图甲可知甲、乙两班中身高的中位数较大的是乙班,图乙输出的S的值为16 |
| D.由图甲可知甲、乙两班中身高的中位数较大的是甲班,图乙输出的S的值为16 |
在两个变量y与x的回归模型中,分别选择了4个不同模型,它们的 如下,其中拟合效果最好的模型是( )
如下,其中拟合效果最好的模型是( )
A.模型1的 为0.975 为0.975 | B.模型2的 为0.79 为0.79 |
C.模型3的 为0.55 为0.55 | D.模型4的 为0.25 为0.25 |
统计某校1000名学生的数学水平测试成绩,得到样本频率分布直方图如图所示,若满分为100分,规定不低于60分为及格,则及格率是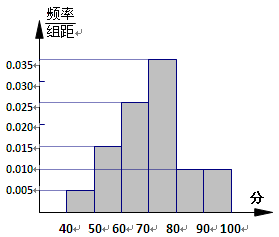
| A.20% |
| B.25% |
| C.6% |
| D.80% |
某班主任对全班50名学生进行了作业量多少的调查,数据如下表:
| | 认为作业多 | 认为作业不多 | 总数 |
| 喜欢玩电脑游戏 | 18 | 9 | 27 |
| 不喜欢玩电脑游戏 | 8 | 15 | 23 |
| 总数 | 26 | 24 | 50 |
 .
. | 0.050 | 0.025 | 0.010 | 0.001 |
 | 3.841 | 5.024 | 6.635 | 10.828 |
参照附表,得到的正确结论是
A.有
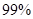 的把握认为“喜欢玩电脑游戏与认为作业量的多少有关系”;
的把握认为“喜欢玩电脑游戏与认为作业量的多少有关系”;B.有
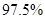 的把握认为“喜欢玩电脑游戏与认为作业量的多少无关系”;
的把握认为“喜欢玩电脑游戏与认为作业量的多少无关系”;C.在犯错误的概率不超过
 的前提下,认为“喜欢玩电脑游戏与认为作业量的多少无关系”;
的前提下,认为“喜欢玩电脑游戏与认为作业量的多少无关系”;D.在犯错误的概率不超过
 的前提下,认为“喜欢玩电脑游戏与认为作业量的多少有关系”.
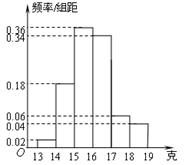
的前提下,认为“喜欢玩电脑游戏与认为作业量的多少有关系”.  ,净重大于等于15克且小于17克的产品数为
,净重大于等于15克且小于17克的产品数为 ,则从频率分布直方图中可分析出
,则从频率分布直方图中可分析出