题目内容
已知函数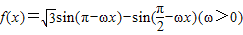 的图象两相邻最高点的坐标分别为
的图象两相邻最高点的坐标分别为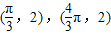 .
.(1)求函数解析式;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,且f(A)=2,求
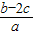 的取值范围.
的取值范围.
【答案】分析:(1)函数f(x)解析式利用诱导公式化简,再利用两角和与差的正弦函数公式化简为一个角的正弦函数,根据题意得出函数的周长,利用周期公式求出ω的值,即可确定出f(x)的解析式;
(2)由f(A)=2,利用特殊角的三角函数值求出A的度数,所求式子利用正弦定理化简,整理后得到最简结果,根据B的范围求出cosB的值域,即可确定出所求式子的范围.
解答:解:(1)f(x)=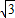 sinωx-cosωx=2sin(ωx-
sinωx-cosωx=2sin(ωx-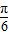 ),
),
∵周期T=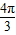 -
-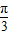 =π=
=π=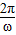 ,∴w=2,
,∴w=2,
则f(x)=2sin(2x-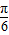 );
);
(2)∵f(A)=2sin(2A-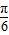 )=2,∴sin(2A-
)=2,∴sin(2A-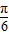 )=1,
)=1,
∵0<A<π,∴-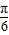 <2A-
<2A-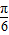 <
<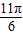 ,
,
∴2A-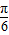 =
= ,即A=
,即A=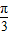 ,
,
由正弦定理得: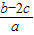 =
=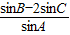 =
=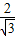 [sinB-2sin(
[sinB-2sin(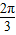 -B)]=-2cosB,
-B)]=-2cosB,
∵0<B<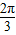 ,∴-
,∴- <cosB<1,
<cosB<1,
则-2<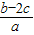 <1.
<1.
点评:此题考查了两角和与差的正弦函数公式,正弦定理,余弦函数的定义域与值域,以及三角函数的周期性及其求法,熟练掌握公式及定理是解本题的关键.
(2)由f(A)=2,利用特殊角的三角函数值求出A的度数,所求式子利用正弦定理化简,整理后得到最简结果,根据B的范围求出cosB的值域,即可确定出所求式子的范围.
解答:解:(1)f(x)=
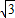 sinωx-cosωx=2sin(ωx-
sinωx-cosωx=2sin(ωx-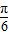 ),
),∵周期T=
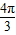 -
-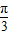 =π=
=π=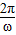 ,∴w=2,
,∴w=2,则f(x)=2sin(2x-
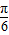 );
);(2)∵f(A)=2sin(2A-
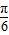 )=2,∴sin(2A-
)=2,∴sin(2A-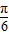 )=1,
)=1,∵0<A<π,∴-
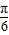 <2A-
<2A-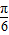 <
<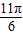 ,
,∴2A-
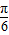 =
= ,即A=
,即A=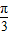 ,
,由正弦定理得:
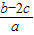 =
=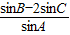 =
=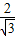 [sinB-2sin(
[sinB-2sin(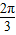 -B)]=-2cosB,
-B)]=-2cosB,∵0<B<
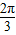 ,∴-
,∴- <cosB<1,
<cosB<1,则-2<
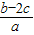 <1.
<1.点评:此题考查了两角和与差的正弦函数公式,正弦定理,余弦函数的定义域与值域,以及三角函数的周期性及其求法,熟练掌握公式及定理是解本题的关键.

练习册系列答案
相关题目
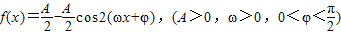 的图象过点(1,2),相邻两条对称轴间的距离为2,且f(x)的最大值为2.
的图象过点(1,2),相邻两条对称轴间的距离为2,且f(x)的最大值为2. 的图象与x轴的两个相邻交点的距离等于
的图象与x轴的两个相邻交点的距离等于 ,若将函数y=f(x)的图象向左平移
,若将函数y=f(x)的图象向左平移 个单位长度得到函数y=g(x)的图象,则y=g(x)的解析式是( )
个单位长度得到函数y=g(x)的图象,则y=g(x)的解析式是( )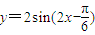
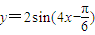
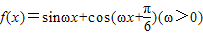 的图象上相邻两条对称轴间的距离为π,则f(x)的一个单调减区间是( )
的图象上相邻两条对称轴间的距离为π,则f(x)的一个单调减区间是( )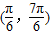
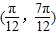

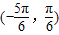
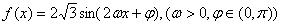 的图象中相邻两条对称轴间的距离为
的图象中相邻两条对称轴间的距离为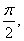 且点
且点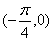 是它的一个对称中心.
是它的一个对称中心.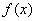 的表达式;
的表达式;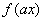
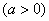 在(0,
在(0,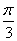 )上是单调递减函数,求
)上是单调递减函数,求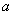 的最大值.
的最大值.