题目内容
已知椭圆C: 中,
中, ,以原点为圆心,椭圆的长半轴为半径的圆与直线
,以原点为圆心,椭圆的长半轴为半径的圆与直线 相切.
相切.
(1)求椭圆C的方程;
(2)若过点M(2,0)的直线与椭圆C相交于A,B, ,设P为椭圆上一点,且满足
,设P为椭圆上一点,且满足 (O为坐标原点),求实数t的值.
(O为坐标原点),求实数t的值.
解:(1)易得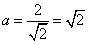 ,又
,又
所以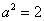 ,
,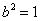 .故方程为
.故方程为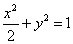
(2)由题意知,直线AB的斜率存在,设直线AB方程: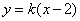
显然,当k=0时,|AB|=2 与已知不符,所以k
与已知不符,所以k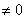 .
.
设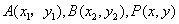
由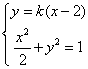 得
得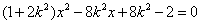
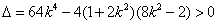 ,
,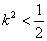 ... 分
... 分
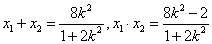
∵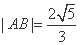 ,∴
,∴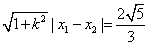 ,∴
,∴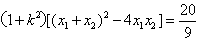
∴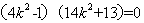 ,即
,即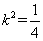 ..
..
又因为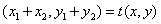 ,且k
,且k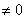 ,即t
,即t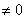
所以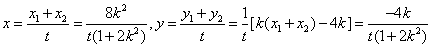
∵点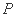 在椭圆上,∴
在椭圆上,∴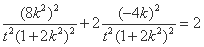 ,又
,又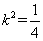 .
.
所以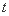 =
=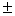
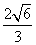 …
…

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 和椭圆
和椭圆 有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为 .
有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为 .  的方程为
的方程为 ,则点
,则点 到直线
到直线 的最小正周期是
的最小正周期是 ,若其图象向右平移
,若其图象向右平移 个单位后得到的函数为奇函数,则函数f(x)的图象
个单位后得到的函数为奇函数,则函数f(x)的图象 对称 B.关于直线
对称 B.关于直线 对称
对称 对称 D.关于直线
对称 D.关于直线 对称
对称
 时,求函数f(x)的最大值和最小值及相应的x的值.
时,求函数f(x)的最大值和最小值及相应的x的值. A.2014
A.2014 中,内角
中,内角 所对的边分别为
所对的边分别为 ,且
,且 边上的高为
边上的高为 ,则
,则 取得最大值时,内角
取得最大值时,内角 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 (B)
(B)
 (D)
(D)
 .
.