Question

【题目】已知函数f（x）=cos ，g（x）=exf（x），其中e为自然对数的底数．
（1）求曲线y=g（x）在点（0，g（0））处的切线方程；
（2）若对任意 时，方程g（x）=xf（x）的解的个数，并说明理由．

Answer 1

【答案】
（1）解：由题意得，f（x）=sinx，g（x）=exsinx，

∴g（0）=e0sin0=0；

g'（x）=ex（cosx+sinx），∴g'（0）=1；

故曲线y=g（x）在点（0，g（0））处的切线方程为y=x

（2）解：设H（x）=g（x）﹣xf（x）， ；

则当 时，

H'（x）=ex（cosx+sinx）﹣sinx﹣xcosx=（ex﹣x）cosx﹣（ex﹣1）sinx，

当 ，显然有 ；

当 时，由 ，

即有 ，

即有H'（x）＜0，

所以当 时，总有H'（x）＜0，

故H（x）在 上单调递减，

故函数H（x）在 上至多有一个零点；

又 ， ；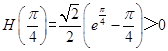

且H（x）在 上是连续不断的，

故函数H（x）在 上有且只有一个零点

【解析】（1）利用导数的几何意义即可求出曲线y=g（x）在点（0，g（0））处的切线方程；（2）构造函数H（x）=g（x）﹣xf（x）， ；利用导数判断函数的单调性，
根据根的存在性定理即可判断函数H（x）在 上零点的个数．