题目内容
【题目】已知椭圆![]() ,直线
,直线![]() 不过原点
不过原点![]() 且不平行于坐标轴,
且不平行于坐标轴,![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() .
.
(1)证明:直线![]() 的斜率与
的斜率与![]() 的斜率的乘积为定值;
的斜率的乘积为定值;
(2)若![]() 过点
过点![]() ,延长线段
,延长线段![]() 与
与![]() 交于点
交于点![]() ,四边形
,四边形![]() 能否为平行四边形?若能,求出
能否为平行四边形?若能,求出![]() 的方程;若不能,说明理由.
的方程;若不能,说明理由.
【答案】⑴见解析⑵四边形OAPB能为平行四边形,![]() 或
或![]() .
.
【解析】
(1)设直线![]() (
(![]() ),
),![]() ,
,![]() ,
,![]() ,通过直线与椭圆联立及坐标表示向量即可证得结论;
,通过直线与椭圆联立及坐标表示向量即可证得结论;
(2)由⑴得OM的方程为![]() .设点P的横坐标为
.设点P的横坐标为![]() ,通过直线与椭圆联立解得
,通过直线与椭圆联立解得![]() ,根据题意有
,根据题意有![]() ,解方程即可得解.
,解方程即可得解.
⑴设直线![]() (
(![]() ),
),![]() ,
,![]() ,
,![]() ,
,
将![]() 代入
代入![]() 中,得
中,得![]() ,
,
故![]() ,
,![]() ,
,
于是直线OM的斜率![]() ,即
,即![]() ,所以命题得证.
,所以命题得证.
⑵四边形OAPB能为平行四边形.
因为直线![]() 过点
过点![]() ,所以
,所以![]() 不过原点且与C有两个交点的充要条件是
不过原点且与C有两个交点的充要条件是![]() 且
且![]() .
.
由⑴得OM的方程为![]() .设点P的横坐标为
.设点P的横坐标为![]() .
.
由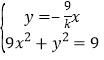 ,得
,得![]() ,即
,即![]() .
.
将点![]() 的坐标代入直线
的坐标代入直线![]() 的方程得
的方程得![]() ,因此
,因此![]() ,
,
四边形OAPB为平行四边形当且仅当线段AB与线段OP互相平分,即![]() .
.
于是![]() ,
,
解得![]() ,
,![]() .所以当四边形OAPB为平行四边形时,l的方程为
.所以当四边形OAPB为平行四边形时,l的方程为![]() 或
或![]() .
.

练习册系列答案
相关题目
【题目】某二手交易市场对某型号的二手汽车的使用年数![]() (
(![]() )与销售价格
)与销售价格![]() (单位:万元/辆)进行整理,得到如下的对应数据:
(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
销售价格 | 16 | 13 | 9.5 | 7 | 4.5 |
(I)试求![]() 关于
关于![]() 的回归直线方程
的回归直线方程![]() .
.
(参考公式: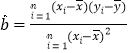 ,
,![]() )
)
(II)已知每辆该型号汽车的收购价格为![]() 万元,根据(I)中所求的回归方程,预测
万元,根据(I)中所求的回归方程,预测![]() 为何值时,销售一辆该型号汽车所获得的利润
为何值时,销售一辆该型号汽车所获得的利润![]() 最大?(利润=销售价格-收购价格)
最大?(利润=销售价格-收购价格)
【题目】为了解某冷饮店的经营状况,随机记录了该店![]() 月的月营业额
月的月营业额![]() (单位:万元)与月份
(单位:万元)与月份![]() 的数据,如下表:
的数据,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 关于
关于![]() 的回归直线方程
的回归直线方程![]() ;
;
(2)若在这样本点中任取两点,求恰有一点在回归直线上的概率.
附:回归直线方程![]() 中,
中,

 ,
,![]() .
.